Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Home
Bookshelves
Mathematics
Geometry
7: Similarity
7.14: Theorems Involving Similarity

7.14: Theorems Involving Similarity

Last updated

Nov 28, 2020
Save as PDF
- 7.13: Proportions and Angle Bisectors
- 7.15: Dilation of a Shape

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Prove and use the Triangle Proportionality, Triangle Angle Bisector, and Pythagorean Theorems.

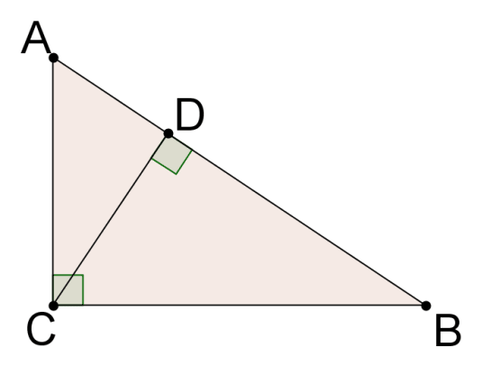
Can you find any similar triangles in the picture below?

Theorems on Similar Triangles

If two triangles are similar, then their corresponding angles are congruent and their corresponding sides are proportional. There are many theorems about triangles that you can prove using similar triangles.

Triangle Proportionality Theorem: A line parallel to one side of a triangle divides the other two sides of the triangle proportionally. This theorem and its converse will be explored and proved in #1 and #2, and the Review exercises.
Triangle Angle Bisector Theorem: The angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle. This theorem will be explored and proved in #3.
Pythagorean Theorem: For a right triangle with legs a and b and hypotenuse c, $a^2+b^2=c^2$ . This theorem will be explored and proved in the Examples problems.

Let's take a look at some problems about proving triangle similarity.

1. Prove that $\Delta ADE\sim \Delta ABC$ .

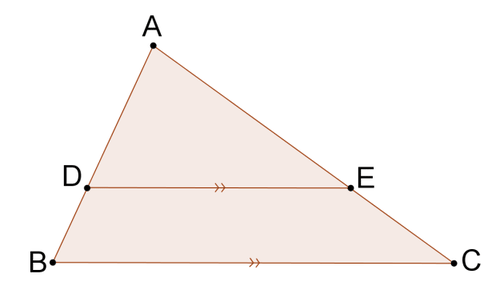
The two triangles share $\angle A$ . Because $\overline{DE}\parallel \overline{BC}$ , corresponding angles are congruent. Therefore, $\angle ADE\cong \angle ABC$ . The two triangles have two pairs of congruent angles. Therefore, $\Delta ADE\sim \Delta ABC$ by AA\sim\).

2. Use your result from #1 to prove that $\dfrac{AB}{AD}=\dfrac{AC}{AE}$ . Then, use algebra to show that $\dfrac{DB}{AD}=\dfrac{EC}{AE}$ .

$\Delta ADE\sim \Delta ABC$ which means that corresponding sides are proportional. Therefore, $\dfrac{AB}{AD}=\dfrac{AC}{AE}$ . Now, you can use algebra to show that the second proportion must be true. Remember that $AB=AD+DB$ and $AC=AE+EC$ .

$\begin{aligned}\dfrac{AB}{AD}&=\dfrac{AC}{AE} \\ \rightarrow \dfrac{AD+DB}{AD}&=AE+\dfrac{EC}{AE} \\ \rightarrow 1+\dfrac{DB}{AD}&=1+\dfrac{EC}{AE} \\ \rightarrow \dfrac{DB}{AD}&=\dfrac{EC}{AE}\end{aligned}$

You have now proved the triangle proportionality theorem: a line parallel to one side of a triangle divides the other two sides of the triangle proportionally.

3. Consider $\Delta ABC$ with $\overline{AE}$ the angle bisector of $\angle BAC$ and point $D$ constructed so that $\overline{DC}\parallel \overline{AE}$ . Prove that $\dfrac{EB}{BA}=\dfrac{EC}{CA}$ .

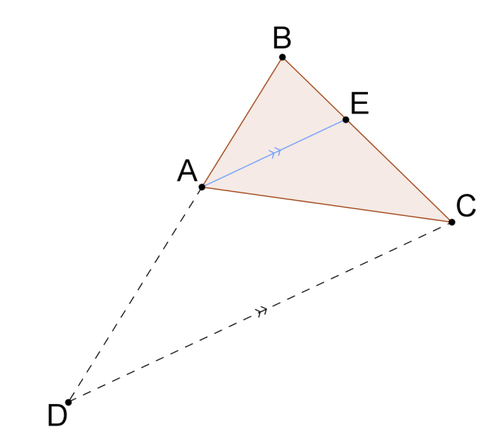
By the triangle proportionality theorem, $\dfrac{EB}{EC}=\dfrac{BA}{AD}$ . Multiply both sides of this proportion by $\dfrac{EC}{BA}$ .

$\begin{aligned}(\dfrac{EC}{BA})\cdot \dfrac{EB}{EC} \\ \rightarrow \dfrac{EB}{BA}=\dfrac{BA}{AD}\cdot (\dfrac{EC}{BA})=\dfrac{EC}{AD}\end{aligned}$

Now all you need to show is that $AD=CA$ in order to prove the desired result.

Because $\overline{AE}$ is the angle bisector of $\angle BAC$ , $\angle BAE\cong \angle EAC$ .
Because $\overline{DC}\parallel \overline{AE}$ , $\angle BAE\cong \angle BDC$ (corresponding angles).
Because $\overline{DC}\parallel \overline{AE}$ , $\angle EAC\cong \angle DCA$ (alternate interior angles).
Thus, $\angle BDC\cong \angle DCA$ by the transitive property.

Therefore, $\Delta ADC$ is isosceles because its base angles are congruent and it must be true that $\overline{AD}\cong \overline{CA}$ . This means that $AD=CA$ . Therefore:

$\dfrac{EB}{BA}=\dfrac{EC}{CA}$

This proves the triangle angle bisector theorem: the angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle.

Example $\PageIndex{1}$

Earlier, you were asked can you find any similar triangles in the picture below.

Solution

There are three triangles in this picture: $\Delta BAC$ , $\Delta BCD$ , $\Delta CAD$ . All three triangles are right triangles so they have one set of congruent angles (the right angle). $\Delta BAC$ and $\Delta BCD$ share $\angle B$ , so $\Delta BAC\sim \Delta BCD by \(AA\sim$ . Similarly, $\Delta BAC$ and $\Delta CAD$ share $\angle C$ , so $\Delta BAC\sim \Delta CAD$ by $AA\sim$ . By the transitive property, all three triangles must be similar to one another.

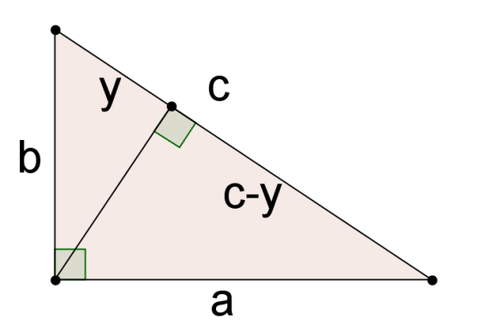
The large triangle above has sides $a$ , $b$ , and $c$ . Side $c$ has been divided into two parts: $y$ and $c−y$ . In the Concept Problem Revisited you showed that the three triangles in this picture are similar.

Example $\PageIndex{2}$

Explain why $\dfrac{a}{c}=\dfrac{c-y}{a}$ .

Solution

When triangles are similar, corresponding sides are proportional. Carefully match corresponding sides and you see that $\dfrac{a}{c}=\dfrac{c-y}{a}$ .

Example $\PageIndex{3}$

Explain why $\dfrac{b}{c}=\dfrac{y}{b}$ .

Solution

When triangles are similar, corresponding sides are proportional. Carefully match corresponding sides and you see that $\dfrac{b}{c}=\dfrac{y}{b}$ .

Example $\PageIndex{4}$

Use the results from #2 and #3 to show that $a^2+b^2=c^2$ .

Solution

Cross multiply to rewrite each equation. Then, add the two equations together.

$\begin{aligned} \dfrac{a}{c}&=\dfrac{c-y}{a}\rightarrow a^2=c^2−cy \\ \dfrac{b}{c}&=\dfrac{y}{b}\rightarrow b^2=cy \\ \rightarrow a^2+b^2&=c^2−cy+cy \\ \rightarrow a^2+b^2&=c^2 \end{aligned}$

You have just proved the Pythagorean Theorem using similar triangles.

Review

Solve for $x$ in each problem.

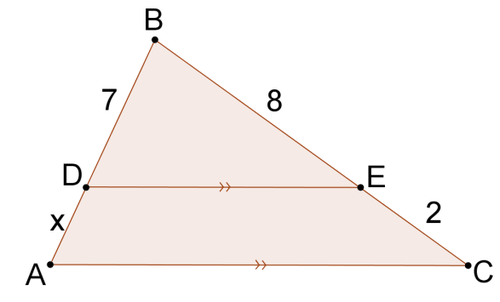
Figure $\PageIndex{6}$
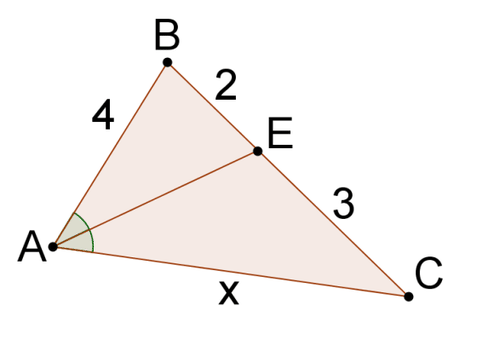
Figure $\PageIndex{7}$
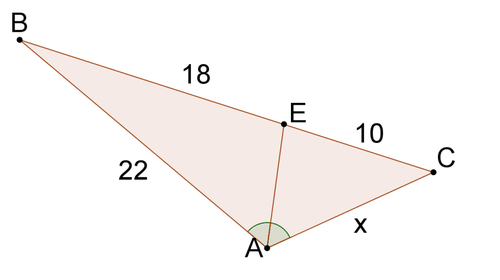
Figure $\PageIndex{8}$
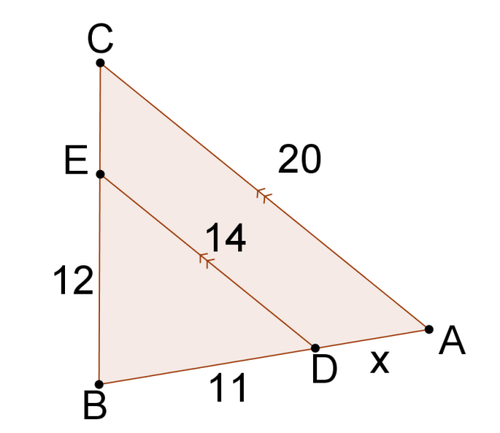
Figure $\PageIndex{9}$
Figure $\PageIndex{10}$
Figure $\PageIndex{11}$
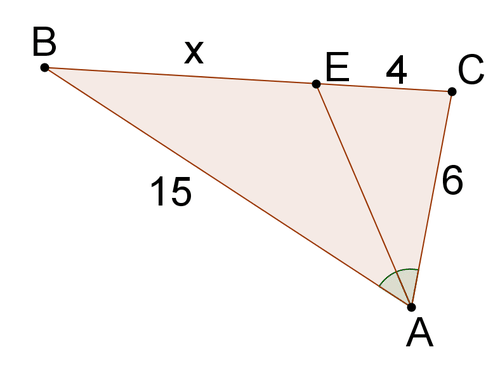
Figure $\PageIndex{12}$

Use the picture below for #8-#10.

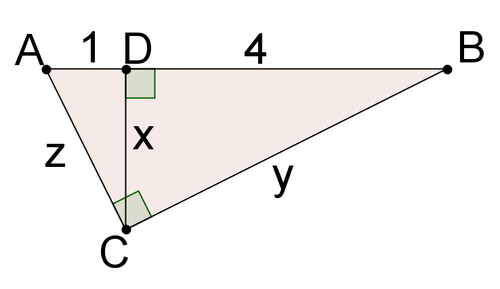
8. Solve for $x$ .

9. Solve for $z$ .

10. Solve for $y$ .

Use the picture below for #11-#13.

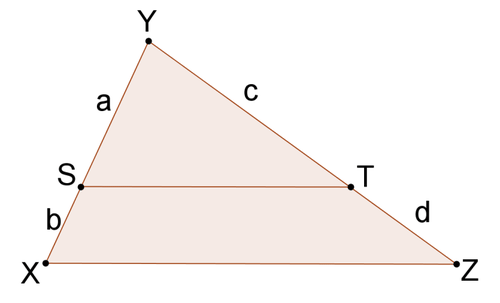
11. Assume that $\dfrac{b}{a}=\dfrac{d}{c}$ . Use algebra to show that $\dfrac{b+a}{a}=\dfrac{d+c}{c}$ .

12. Prove that $\Delta YST\sim \Delta YXZ$

13. Prove that $\overline{ST}\parallel \overline{XZ}$

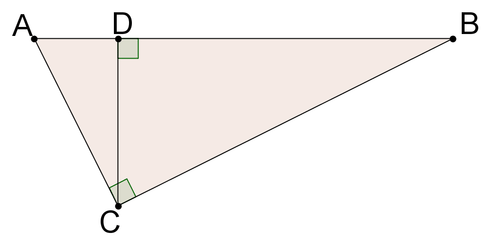
14. Prove that a segment that connects the midpoints of two sides of a triangle will be parallel to the third side of the triangle.

15. Prove the Pythagorean Theorem using the picture below.

Review (Answers)

To see the Review answers, open this PDF file and look for section 6.6.

Vocabulary

Term	Definition
Pythagorean Theorem	The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by $a^2+b^2=c^2$ , where $a$ and $b$ are legs of the triangle and $c$ is the hypotenuse of the triangle.
Triangle Proportionality Theorem	The Triangle Proportionality Theorem states that if a line is parallel to one side of a triangle and it intersects the other two sides, then it divides those sides proportionally.
Triangle Angle Bisector Theorem	The angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle.

Theorems on Similar Triangles

Review

Review (Answers)

Vocabulary

Support Center

How can we help?