4.15: ASA and AAS
- Page ID
- 4812
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two sets of corresponding angles and any corresponding set of sides prove congruent triangles.
Angle-Side-Angle Postulate and Angle-Angle-Side Theorem
If two angles and one side in one triangle are congruent to the corresponding two angles and one side in another triangle, then the two triangles are congruent. This idea encompasses two triangle congruence shortcuts: Angle-Side-Angle and Angle-Angle-Side.
Angle-Side-Angle (ASA) Congruence Postulate: If two angles and the included side in one triangle are congruent to two angles and the included side in another triangle, then the two triangles are congruent.
Angle-Angle-Side (AAS) Congruence Theorem: If two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle, then the triangles are congruent.
The placement of the word Side is important because it indicates where the side that you are given is in relation to the angles. The pictures below help to show the difference between the two shortcuts.
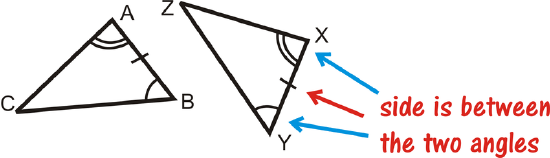
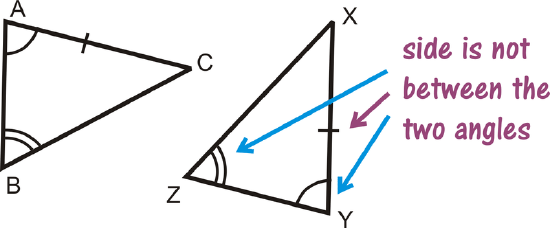
What if you were given two triangles and provided with only the measure of two of their angles and one of their side lengths? How could you determine if the two triangles were congruent?
Example \(\PageIndex{1}\)
Can you prove that the following triangles are congruent? Why or why not?
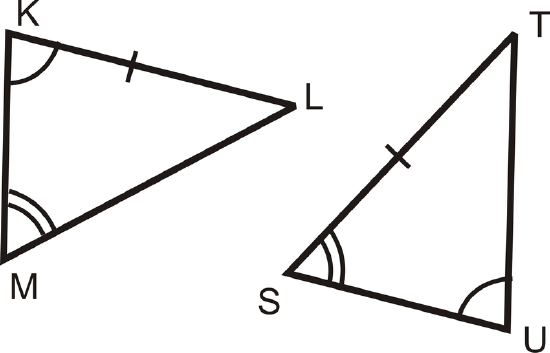
Solution
We cannot show the triangles are congruent because \(\overline{KL}\) and \(\overline{ST}\) are not corresponding, even though they are congruent. To determine if \(\(\overline{KL}\) and \(\overline{ST}\) are corresponding, look at the angles around them, \(\(\angle K\) and \(\angle L\) and \angle S\) and \(\angle T\). \(\angle K\) has one arc and \angle L is unmarked. \(\angle S\) has two arcs and \(\angle T\) is unmarked. In order to use AAS, \(\angle S\) needs to be congruent to \(\angle K\).
Example \(\PageIndex{2}\)
Write a 2-column proof.
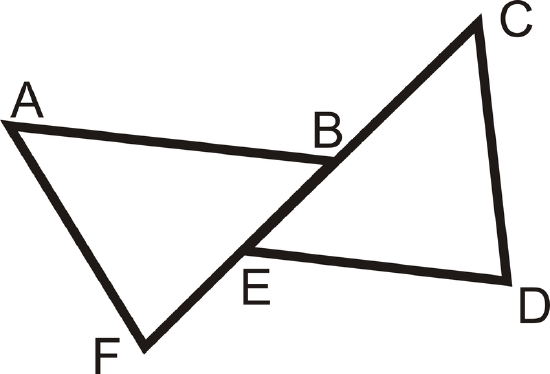
Given: \(\overline{AB}\parallel \overline{ED}\), \(\angle C\cong \angle F\), \(\overline{AB}\cong \overline{ED}\)
Prove: \(\overline{AF}\cong \overline{CD}\)
Solution
| Statement | Reason |
|---|---|
| 1. \(\overline{AB}\parallel \overline{ED}\), \(\angle C\cong \angle F\), \(\overline{AB}\cong \overline{ED}\) | 1. Given |
| 2. \(\angle ABE\cong \angle DEB\) | 2. Alternate Interior Angles Theorem |
| 3. \(\Delta ABF\cong \Delta DEC\) | 3. ASA |
| 4. \(\overline{AF}\cong \overline{CD}\) | 4. CPCTC (Corresponding Parts of Congruent Triangles are Congruent) |
Example \(\PageIndex{3}\)
What information do you need to prove that these two triangles are congruent using the ASA Postulate, \(\overline{AB}\cong UT\overline{AB}\), \(\overline{AC}\cong \overline{UV}\), \(\overline{BC}\cong \overline{TV}\), or \(\angle B\cong \angle T\)?
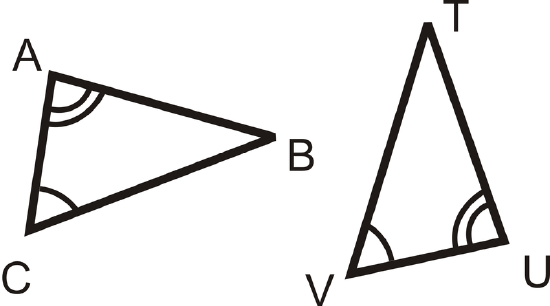
Solution
For ASA, we need the side between the two given angles, which is \(\overline{AC}\) and \(\overline{UV}\). The answer is \(\overline{AC}\cong \overline{UV}\).
Example \(\PageIndex{4}\)
Write a 2-column proof.
Given: \(\angle C\cong \angle E\), \(\overline{AC}\cong \overline{AE}\)
Prove: \(\Delta ACF\cong \Delta AEB \)
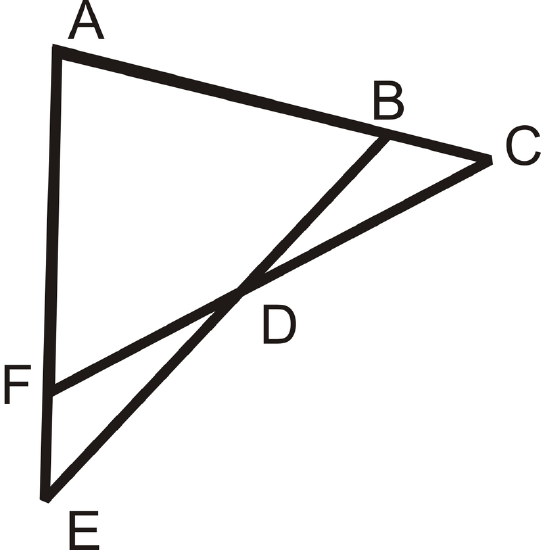
Solution
| Statement | Reason |
|---|---|
| 1. \(\angle C\cong \angle E\), \(\overline{AC}\cong \overline{AE}\) | 1. Given |
| 2. \(\angle A\cong \angle A\) | 2. Reflexive \(PoC\) |
| 3. \(\Delta ACF \cong \Delta AEB\) | 3. ASA |
Example \(\PageIndex{5}\)
What information do you need to prove that these two triangles are congruent using ASA? AAS?
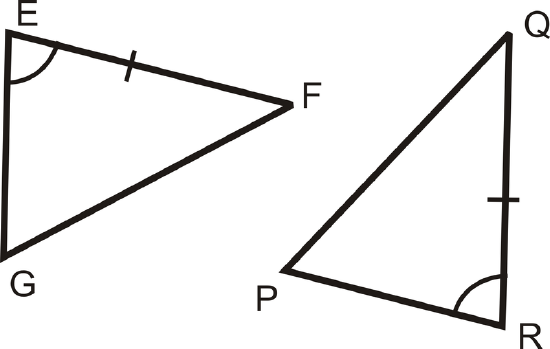
Solution
For ASA, we need the angles on the other side of \(\overline{EF}\) and \(\overline{QR}\). \(\angle F\cong \angle Q\)
For AAS, we would need the other angle. \(\angle G\cong \angle P\)
Review
For questions 1-3, determine if the triangles are congruent. If they are, write the congruence statement and which congruence postulate or theorem you used.
-
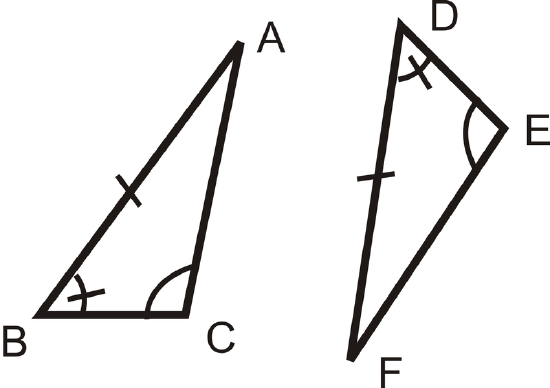
Figure \(\PageIndex{8}\) -
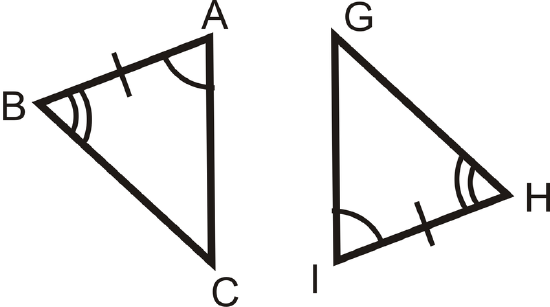
Figure \(\PageIndex{9}\) -
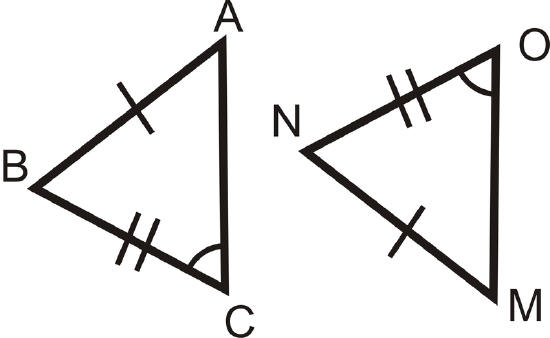
Figure \(\PageIndex{10}\)
For questions 4-8, use the picture and the given information below.
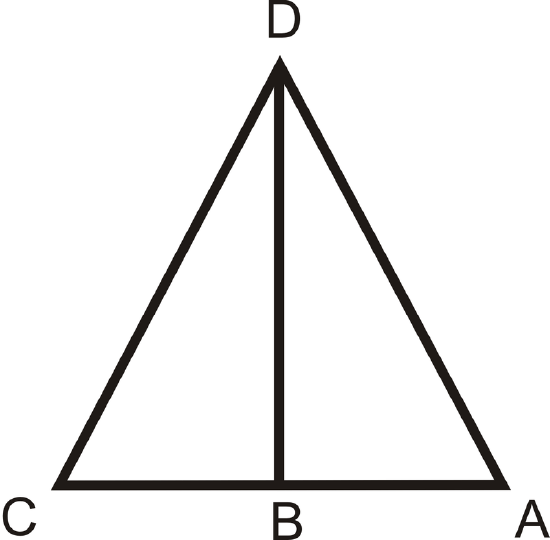
Given: \(\overline{DB}\perp \overline{AC}\), \(\overline{DB}\) is the angle bisector of \(\angle CDA\)
- From \(\overline{DB}\perp \overline{AC}\), which angles are congruent and why?
- Because \(\overline{DB}\) is the angle bisector of \(\angle CDA\), what two angles are congruent?
- From looking at the picture, what additional piece of information are you given? Is this enough to prove the two triangles are congruent?
- Write a 2-column proof to prove \(\Delta CDB\cong \Delta ADB\), using #4-6.
- What would be your reason for \(\angle C\cong \angle A\)?
For questions 9-13, use the picture and the given information.
Given: \(\overline{LP}\parallel \overline{NO}\), \(\overline{LP}\cong \overline{NO}\)
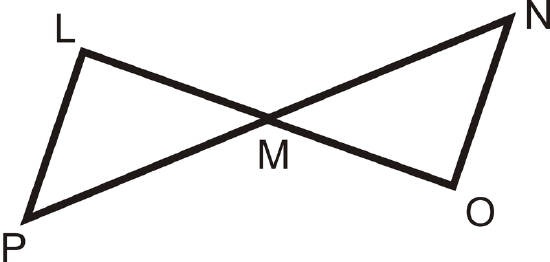
- From \(\overline{LP}\parallel \overline{NO}\), which angles are congruent and why?
- From looking at the picture, what additional piece of information can you conclude?
- Write a 2-column proof to prove \(\Delta LMP\cong \Delta OMN\).
- What would be your reason for \(\overline{LM}\cong \overline{MO}\)?
- Fill in the blanks for the proof below. Use the given from above. Prove: \(M\) is the midpoint of \(\overline{PN}\).
| Statement | Reason |
|---|---|
| 1. \(\overline{LP}\parallel \overline{NO}\), \(\overline{LP}\cong \overline{NO}\) | 1. Given |
| 2. | 2. Alternate Interior Angles |
| 3. | 3. ASA |
| 4. \(\overline{LM}\cong \overline{MO}\) | 4. |
| 5. \(M\) is the midpoint of \(\overline{PN}\). | 5. |
Determine the additional piece of information needed to show the two triangles are congruent by the given postulate.
- AAS
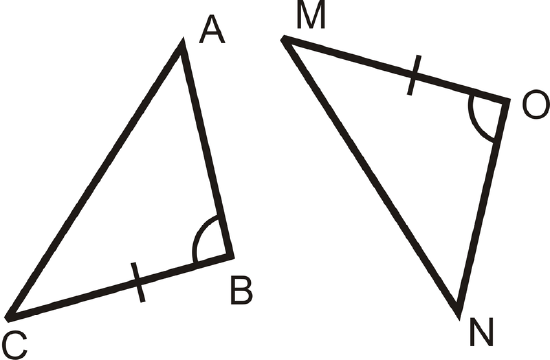
Figure \(\PageIndex{13}\) - ASA

Figure \(\PageIndex{14}\) - ASA
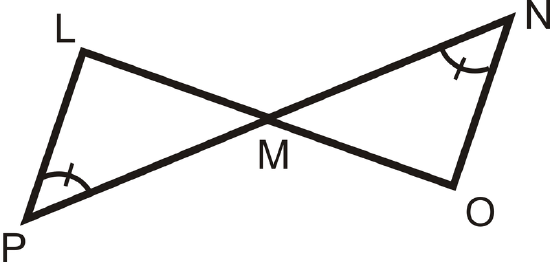
Figure \(\PageIndex{15}\) - AAS

Figure \(\PageIndex{16}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.8.
Resources
Vocabulary
| Term | Definition |
|---|---|
| CPCTC | Corresponding Parts of Congruent Triangles are Congruent. It is used to show two sides or two angles in triangles are congruent after having proved that the triangles are congruent. |
| AAS (Angle-Angle-Side) | If two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle, then the triangles are congruent. |
| Angle Side Angle Triangle | The term 'angle-side-angle triangle' refers to a triangle with known measures of two angles and the length of the side between them. |
| ASA | ASA, angle-side-angle, refers to two known angles in a triangle with one known side between the known angles. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Triangle Congruence | Triangle congruence occurs if 3 sides in one triangle are congruent to 3 sides in another triangle. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Video: Introduction to Congruent Triangles
Activities: ASA and AAS Triangle Congruence Discussion Questions
Study Aids: Triangle Congruence Study Guide
Practice: ASA and AAS
Real World: SSS Triangle Congruence

