Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Home
Bookshelves
Mathematics
Geometry
8: Rigid Transformations
8.8: Translation Applications in Circle Similarity

8.8: Translation Applications in Circle Similarity

Last updated

Jun 15, 2022
Save as PDF
- 8.7: Geometry Software for Translations
- 8.9: Translation Notation

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Solve problems involving ratios and circles and use transformations to show circles are similar.

Circles and Similarity

Sean has two circles, one with a radius of 1 inch and another with a radius of 3 inches.

What is the ratio between the radii of the circles?
What is the scale factor between the two circles?
What is the ratio between the circumferences of the circles?
What is the ratio between the areas of the circles?
What do area ratios and circumference ratios have to do with scale factor?

A circle is a set of points equidistant from a given point. The radius of a circle, r, is the distance from the center of the circle to the circle. A circle's size depends only on its radius.

Two figures are similar if a similarity transformation will carry one figure to the other. A similarity transformation is one or more rigid transformations followed by a dilation. In the examples, you will show that a similarity transformation exists between any two circles and therefore, all circles are similar.

Recall two important formulas related to circles:

Circumference (Perimeter) of a Circle: $C=2\pi r$
Area of a Circle: $A=\pi r^{2}$

Once you have shown that all circles are similar, you will explore how the circumferences and areas of circles are related.

Proving Circle Similarity

Consider circle $A$ , centered at point $A$ with radius $r_A$ , and circle $D$ , centered at point $D$ with radius $rD$ . Perform a rigid transformation to bring point $A$ to point $D$ .

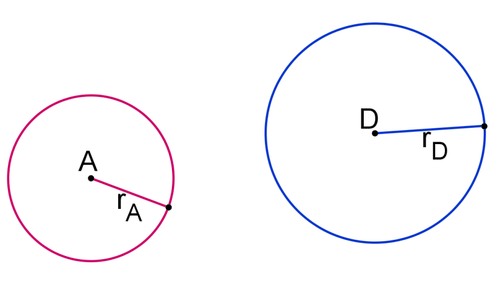
Draw a vector from point $A$ to point $D$ . Translate Circle $A$ \) along the vector to create circle $A′$ . Note that $r_A \cong r′_A$ .

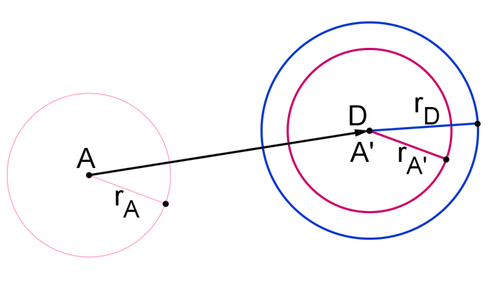
Dilate circle $A$ to map it to circle $D$ . Can you be confident that the circles are similar?

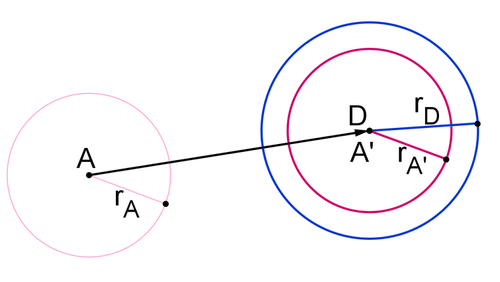
Because the size of a circle is completely determined by its radius, you can use the radii to find the correct scale factor. Dilate circle $A′$ about point $A′$ by a scale factor of $\dfrac{r_D}{r_{A′}}$ .

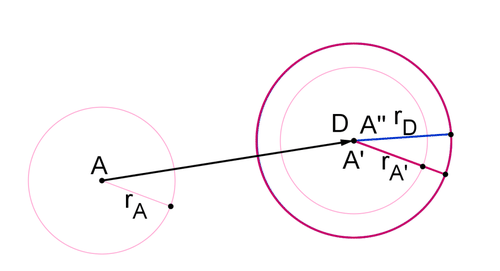
Circle $A′′$ is the same Circle $A$ s circle $D$ . You can be confident of this because $r_{A′′}=\dfrac{r_D}{r_{A′}} \cdot r_{A′}=r_{D}$ and point $A′′$ is the same as point $D$ . Because a circle is defined by its center and radius, if two circles have the same center and radius then they are the same circle.

This means that circle $A$ is similar to circle $D$ , because a similarity transformation (translation then dilation) mapped circle $A$ to circle D\).

Circle $A$ and circle $D$ were two random circles. This proves that in general, all circles are similar.

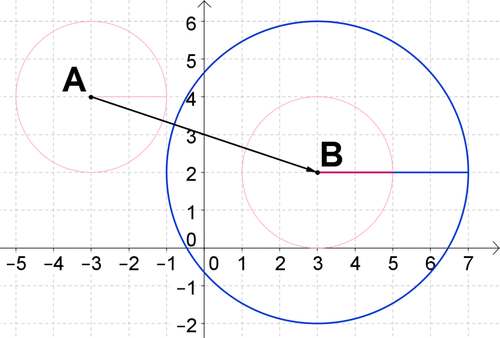
3. Show that circle $A$ with center $(−3, 4)$ and radius 2 is similar to circle $B$ with center $(3, 2)$ and radius 4.

Translate circle $A$ along the vector from $(−3, 4)$ to $(3, 2)$ . Then, dilate the image about its center by a scale factor of 2. You will have mapped circle $A$ to circle $B$ with a similarity transformation. This means that circle $A$ is similar to circle $B$ .

Example $\PageIndex{1}$

Earlier, you were given a problem about Sean and his two circles.

Sean has two circles, one with a radius of 1 inch and another with a radius of 3 inches.

What is the ratio between the radii of the circles?
What is the scale factor between the two circles?
What is the ratio between the circumferences of the circles?
What is the ratio between the area of the circles?
What do area ratios and circumference ratios have to do with scale factor?

Solution

The ratio between the radii is 31.
A scale factor exists because any two circles are similar. You can use the radii to determine the scale factor. The ratio between the radii is $\dfrac{3}{1}$ so the scale factor is $\dfrac{3}{1}=3$ .
The circumference of the smaller circle is $C=2\pi (1)=2\pi$ . The circumference of the larger circle is $C=2\pi (3)=6\pi$ . The ratio between the circumferences is $\dfrac{6\pi}{2\pi}=\dfrac{3}{1}$ .
The area of the smaller circle is $A=\pi (1)2=\pi$ . The area of the larger circle is $A=\pi(3)^2=9\pi$ . The ratio between the areas is $\dfrac{9\pi}{\pi}=\dfrac{9}{1}$ . Note that $\dfrac{9}{1}=(\dfrac{3}{1})^2$ .
The area ratio is the scale factor squared, because area is a two dimensional measurement. The circumference ratio is equal to the scale factor, because circumference is a one dimensional measurement.

Example $\PageIndex{2}$

Show that Circle $A$ with center $(−1,7)$ and radius 2 is similar to Circle $B$ with center $(4,6)$ and radius 3.

Solution

Translate Circle $A$ along the vector from $(−1,7)$ to $(4,6)$ . Then, dilate the image about its center with a scale factor of $\dfrac{3}{2}$ . You will have mapped Circle $A$ to Circle $B$ with a similarity transformation. This means that Circle $A$ is similar to Circle $B$ .

Example $\PageIndex{3}$

The ratio of the circumference of circle $D$ to the circumference of circle $C$ is $\dfrac{4}{3}$ . What is the ratio of their areas?

Solution

The ratio of the circumferences is the same as the scale factor. Therefore, the scale factor is $\dfrac{4}{3}$ . The ratio of the areas is the scale factor squared. Therefore, the ratio of the areas is $(\dfrac{4}{3})^2=\dfrac{16}{9}$ .

Example $\PageIndex{4}$

The ratio of the area of circle $F$ to the area of circle $E$ is $\dfrac{9}{4}$ . What is the ratio of their radii?

Solution

The ratio of the areas is the scale factor squared. Therefore, the scale factor is $\sqrt{\dfrac{9}{4}}=\dfrac{3}{2}$ . The ratio of the radii is the same as the scale factor, so the ratio of the radii is $\dfrac{3}{2}$ .

Review

For #1-#10, show that the circles are similar by describing the similarity transformation necessary to map one circle onto the other.

Circle $A$ with center (2,7)\) and radius 4. Circle $B$ with center $(1,−4)$ and radius 3.
Circle $A$ with center (6,4)\) and radius 3. Circle $B$ with center $(−5,6)$ and radius 5.
Circle $A$ with center (1,4)\) and radius 2. Circle $B$ with center $(3,−2)$ and radius 7.
Circle $A$ with center (8,1)\) and radius 6. Circle $B$ with center $(6,−4)$ and radius 8.
Circle $A$ with center (−2,10)\) and radius 3. Circle $B$ with center $(−1,−4)$ and radius 6.
Circle $A$ with center (−1,5) and radius 4. Circle $B$ with center $(−1,5)$ and radius 5.
Circle $A$ with center (−4,−2) and radius 1. Circle $B$ with center $(1,8)$ and radius 4.
Circle $A$ with center (10,3) and radius 5. Circle $B$ with center $(4,2)$ and radius 8.
Circle $A$ with center (12,4) and radius 10. Circle $B$ with center $(12,4)$ and radius 12.
Circle $A$ with center (−7,6) and radius 9. Circle $B$ with center $(1,−4)$ and radius 9.
The ratio of the circumference of Circle $A$ to the circumference of Circle $B$ is $\dfrac{2}{3}$ . What is the ratio of their radii?
The ratio of the area of Circle $A$ to the area of Circle $B$ is $\dfrac{6}{1}$ . What is the ratio of their radii?
The ratio of the radius of Circle $A$ to the radius of Circle $B$ is $\dfrac{5}{9}$ . What is the ratio of their areas?
The ratio of the area of Circle $A$ to the area of Circle $B$ is $\dfrac{12}{5}$ . What is the ratio of their circumferences?
To show that any two circles are similar you need to perform a translation and/or a dilation. Why won't you ever need to use reflections or rotations?

Review (Answers)

To see the Review answers, open this PDF file and look for section 8.1.

Vocabulary

Term	Definition
Circle	A circle is the set of all points at a specific distance from a given point in two dimensions.
Dilation	To reduce or enlarge a figure according to a scale factor is a dilation.
Radius	The radius of a circle is the distance from the center of the circle to the edge of the circle.
Rigid Transformation	A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure.
Similarity Transformation	A similarity transformation is one or more rigid transformations followed by a dilation.

Additional Resources

Interactive Element

Circles and Similarity

Proving Circle Similarity

Review

Review (Answers)

Vocabulary

Additional Resources

Support Center

How can we help?