8.9: Translation Notation

Graphical introduction to image translations. Learn to use notation to describe mapping rules,and graph images given preimage and translation

Rules for Translations

Jack describes a translation as point moving from \(J(−2, 6)\) to \(J′(4,9)\). Write the mapping rule to describe this translation for Jack.

In geometry, a transformation is an operation that moves, flips, or changes a shape (called the preimage) to create a new shape (called the image). A translation is a type of transformation that moves each point in a figure the same distance in the same direction. Translations are often referred to as slides. You can describe a translation using words like "moved up 3 and over 5 to the left" or with notation. There are two types of notation to know.

1. One notation looks like \(T_{(3, 5)}\). This notation tells you to add 3 to the \(x\) values and add 5 to the \(y\) values.
2. The second notation is a mapping rule of the form \((x,y) \rightarrow (x−7, y+5)\). This notation tells you that the \(x\) and \(y\) coordinates are translated to \(x−7\) and \(y+5\).

The mapping rule notation is the most common.

Interactive Element

Let's write a mapping rule for each of the following translations:

1. Sarah describes a translation as point \(P\) moving from \(P(−2,2)\) to \(P′(1,−1)\).

In general, \(P(x, y) \rightarrow P′(x+a, y+b)\).

In this case, \(P(−2, 2) \rightarrow P′(−2+a, 2+b)\) or \(P(−2, 2) \rightarrow P′(1, −1)\)

Therefore:

\(\begin{array}{rr}
-2+a=1 & \text { and } \quad 2+b=-1 \\
a=3 & \quad b=-3
\end{array}\)

The rule is: \((x,y) \rightarrow (x+3, y−3)\)

2. Mikah describes a translation as point D in a diagram moving from \(D(1, −5)\) to \(D′(−3,1)\).

In general, \(P(x,y) \rightarrow P′(x+a, y+b)\).

In this case, \(D(1,−5) \rightarrow D′(1+a,−5+b)\) or \(D(1,−5) \rightarrow D′(−3,1)\)

Therefore:

\(\begin{array}{rrr}
1+a=-3 & \text { and } & -5+b=1 \\
a=-4 & & b=6
\end{array}\)

The rule is: \((x,y) \rightarrow (x−4, y+6)\)

3. The translation of the preimage \(A\) to the translated image \(J\) in the diagram below:

Figure \(\PageIndex{1}\)

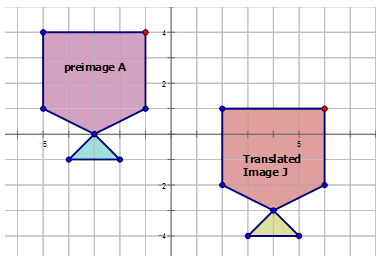
First, pick a point in the diagram to use to see how it is translated.

Figure \(\PageIndex{2}\)

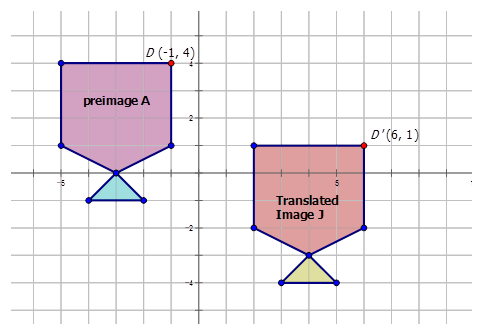
\(D:(−1,4) D′:(6,1)\)

\(D(x,y) \rightarrow D′(x+a,y+b)\)

So: \(D(−1,4) \rightarrow D′(−1+a,4+b)\) or \(D(−1,4) \rightarrow D′(6,1)\)

Therefore:

\(\begin{array}{rrr}
-1+a=6 & \text { and } & 4+b=1 \\
a=7 & & b=-3
\end{array}\)

The rule is: \((x,y) \rightarrow (x+7,y−3)\)

Example \(\PageIndex{1}\)

Earlier, you were told that Jack described a translation as point \(J\) moving from \(J(−2,6)\) to \(J′(4,9)\). What is the mapping rule that describes this translation?

Solution

\((x,y) \rightarrow (x+6, y+3)\)

Example \(\PageIndex{2}\)

Write the mapping rule that represents the translation of the red triangle to the translated green triangle in the diagram below.

Figure \(\PageIndex{3}\)

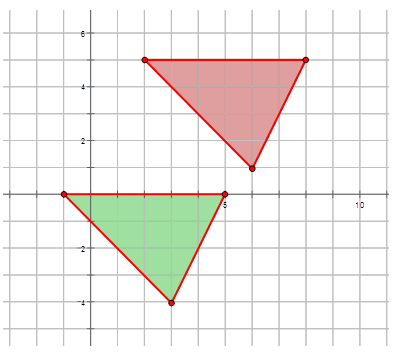
Solution

\((x, y) \rightarrow (x−3, y−5)\)

Example \(\PageIndex{3}\)

The following pattern is part of wallpaper found in a hotel lobby. Write the mapping rule that represents the translation of one blue trapezoid to a translated blue trapezoid shown in the diagram below.

Figure \(\PageIndex{4}\)

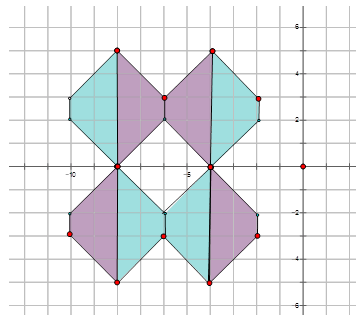
Solution

If you look closely at the diagram below, there two pairs of trapezoids that are translations of each other. Therefore you can choose one blue trapezoid that is a translation of the other and pick a point to find out how much the shape has moved to get to the translated position.

Figure \(\PageIndex{5}\)

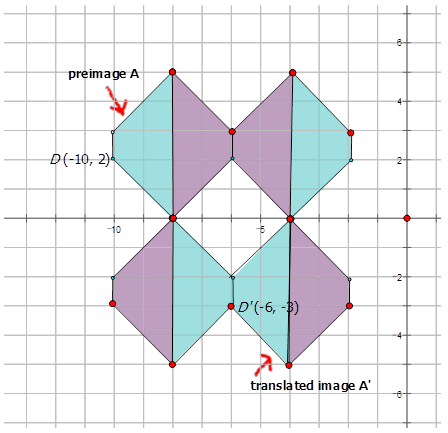
For those two trapezoids: \((x,y) \rightarrow (x+4, y−5)\)

Review

Write the mapping rule to describe the movement of the points in each of the translations below.

1. \(S(1,5) \rightarrow S′(2,7)\)
2. \(W(−5,−1) \rightarrow W′(−3,1)\)
3. \(Q(2,−5) \rightarrow Q′(−6,3)\)
4. \(M(4,3) \rightarrow M′(−2,9)\)
5. \(B(−4,−2) \rightarrow B′(2,−2)\)
6. \(A(2,4) \rightarrow A′(2,6)\)
7. \(C(−5,−3) \rightarrow C′(−3,4)\)
8. \(D(4,−1) \rightarrow D′(−4,2)\)
9. \(Z(7,2) \rightarrow Z′(−3,6)\)
10. \(L(−3,−2) \rightarrow L′(4,−1)\)

Write the mapping rule that represents the translation of the preimage to the image for each diagram below.

11. 

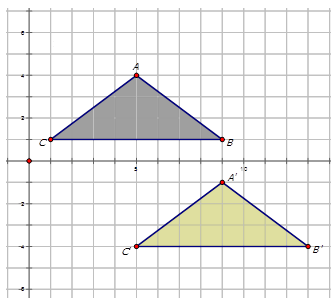
    Figure \(\PageIndex{6}\)

12. 

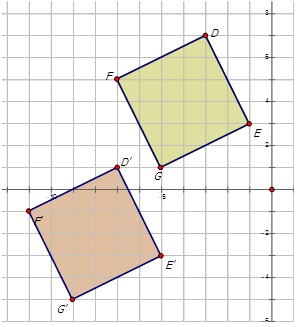
    Figure \(\PageIndex{7}\)

13. 

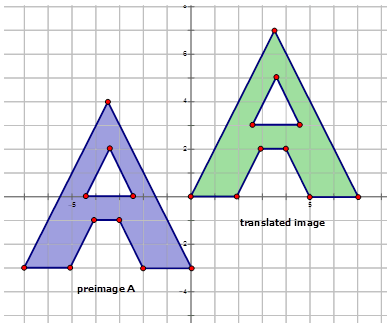
    Figure \(\PageIndex{8}\)

14. 

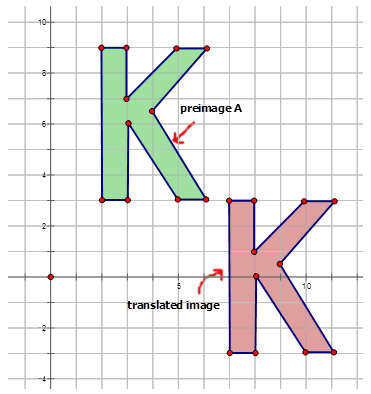
    Figure \(\PageIndex{9}\)

15. 

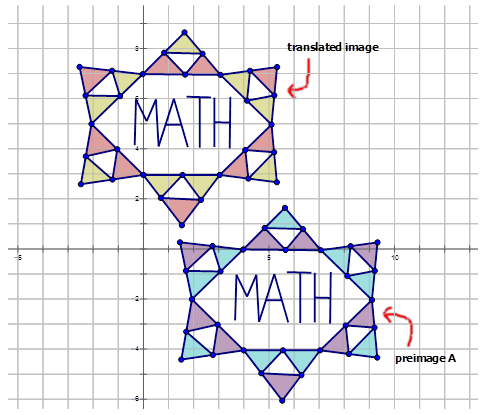
    Figure \(\PageIndex{10}\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 10.3.

Additional Resources

Interactive Element

Video: Quadrants of Coordinate Plane

Practice: Translation Notation