8.10: Defining Rotation
- Page ID
- 6027
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transformations by which a figure is turned around a fixed point to create an image.
Rotations
A transformation is an operation that moves, flips, or otherwise changes a figure to create a new figure. A rigid transformation (also known as an isometry or congruence transformation) is a transformation that does not change the size or shape of a figure.
The rigid transformations are translations, reflections, and rotations. The new figure created by a transformation is called the image. The original figure is called the preimage. If the preimage is \(A\), then the image would be \(A′\), said “a prime.” If there is an image of \(A′\), that would be labeled \(A′′\), said “a double prime.”
A rotation is a transformation where a figure is turned around a fixed point to create an image. The lines drawn from the preimage to the center of rotation and from the center of rotation to the image form the angle of rotation.
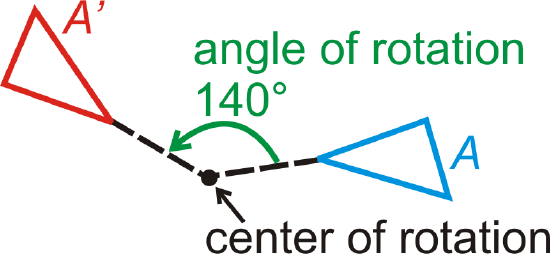
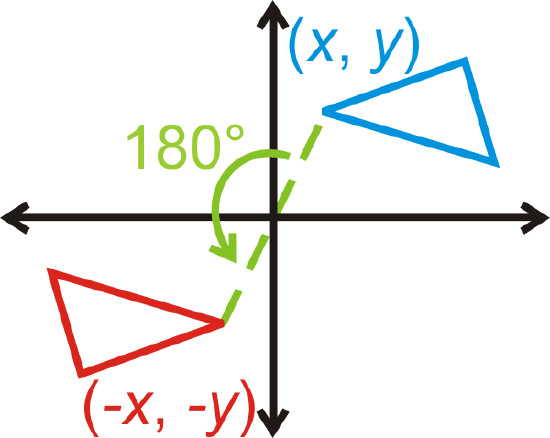
While we can rotate any image any amount of degrees, \(90^{\circ}\), \(180^{\circ}\) and \(270^{\circ}\) rotations are common and have rules worth memorizing.
Rotation of \(180^{\circ}\): \((x,y)\rightarrow (−x,−y)\)
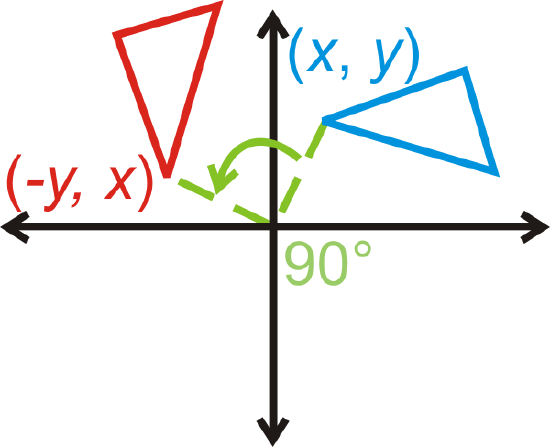
Rotation of \(90^{\circ}\): \((x,y)\rightarrow (−y,x)\)
Rotation of \(270^{\circ}\): \((x,y)\rightarrow (y,−x)\)
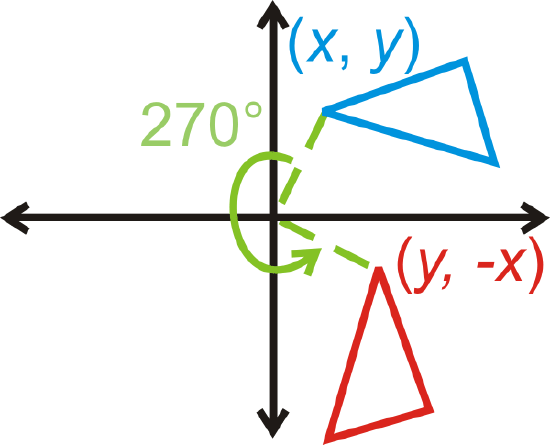
What if you were given the coordinates of a quadrilateral and you were asked to rotate that quadrilateral \(270^{\circ}\) about the origin? What would its new coordinates be?
Example \(\PageIndex{1}\)
A rotation of \(80^{\circ}\) clockwise is the same as what counterclockwise rotation?
Solution
There are \(360^{\circ}\) around a point. So, an \(80^{\circ}\) rotation clockwise is the same as a \(360^{\circ}−80^{\circ}=280^{\circ}\) rotation counterclockwise.
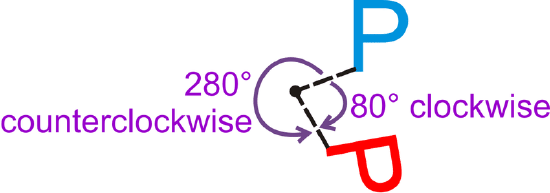Figure \(\PageIndex{6}\)Example \(\PageIndex{2}\)
A rotation of \(160^{\circ} counterclockwise is the same as what clockwise rotation?
Solution
\(360^{\circ}−160^{\circ}=200^{\circ}\) clockwise rotation.
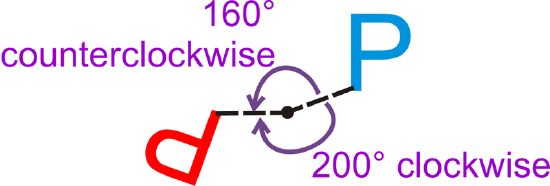
Example \(\PageIndex{3}\)
Rotate \(\overline{ST} 90^{\circ}\).
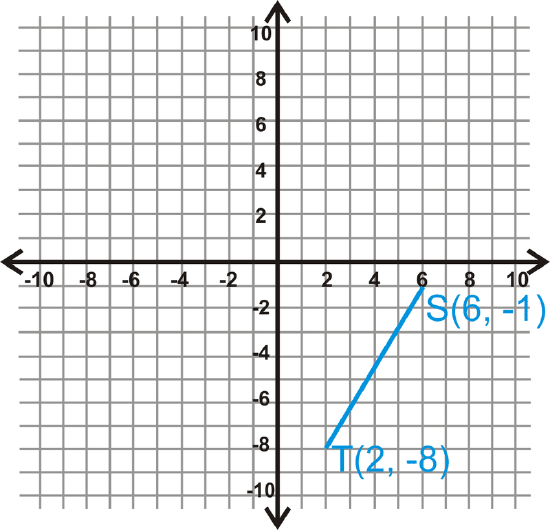
Solution
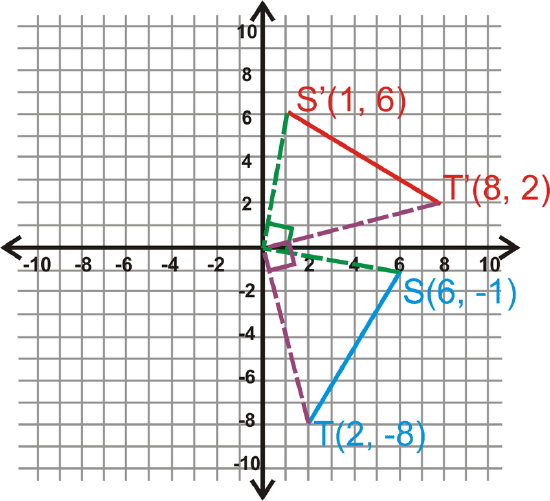
Example \(\PageIndex{4}\)
The rotation of a quadrilateral is shown below. What is the measure of \(x\) and \(y\)?
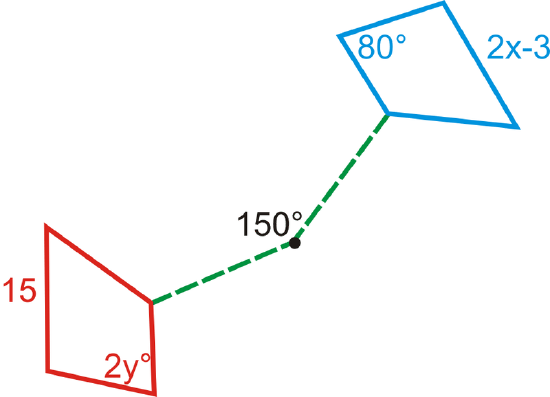
Solution
Because a rotation produces congruent figures, we can set up two equations to solve for \(x\) and \(y\).
\(y=4\begin{array}{rr}
2 y=80^{\circ} & 2 x-3=15 \\
y=40^{\circ} & 2 x=18 \\
& x=9
\end{array}\)
Example \(\PageIndex{5}\)
Rotate \(\Delta ABC\), with vertices \(A(7,4)\), \(B(6,1)\), and \(C(3,1)\), \(180^{\circ}\) about the origin. Find the coordinates of \(\Delta A′B′C′\).
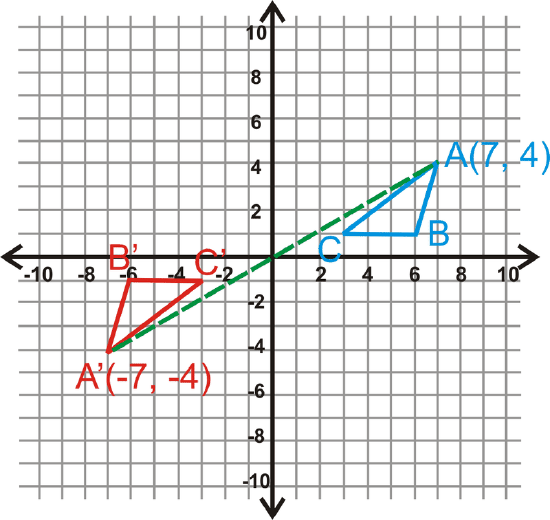
Solution
Use the rule above to find \(\Delta A′B′C′\).
\(\begin{aligned}A(7,4)&\rightarrow A′(−7,−4) \\ B(6,1)&\rightarrow B′(−6,−1) \\ C(3,1)&\rightarrow C′(−3,−1)\end{aligned}\)
Review
In the questions below, every rotation is counterclockwise, unless otherwise stated.
- If you rotated the letter p 180^{\circ}\) counterclockwise, what letter would you have?
- If you rotated the letter p \(180^{\circ}\) c\(ockwise, what letter would you have?
- A \(90^{\circ}\) clockwise rotation is the same as what counterclockwise rotation?
- A \(270^{\circ}\) clockwise rotation is the same as what counterclockwise rotation?
- A \(210^{\circ}\) counterclockwise rotation is the same as what clockwise rotation?
- A \(120^{\circ}\) counterclockwise rotation is the same as what clockwise rotation?
- A \(340^{\circ}\) counterclockwise rotation is the same as what clockwise rotation?
- Rotating a figure \(360^{\circ}\) is the same as what other rotation?
- Does it matter if you rotate a figure \(180^{\circ}\) clockwise or counterclockwise? Why or why not?
- When drawing a rotated figure and using your protractor, would it be easier to rotate the figure \(300^{\circ}\) counterclockwise or \(60^{\circ}\) clockwise? Explain your reasoning.
Rotate each figure in the coordinate plane the given angle measure. The center of rotation is the origin.
- \(180^{\circ}\)
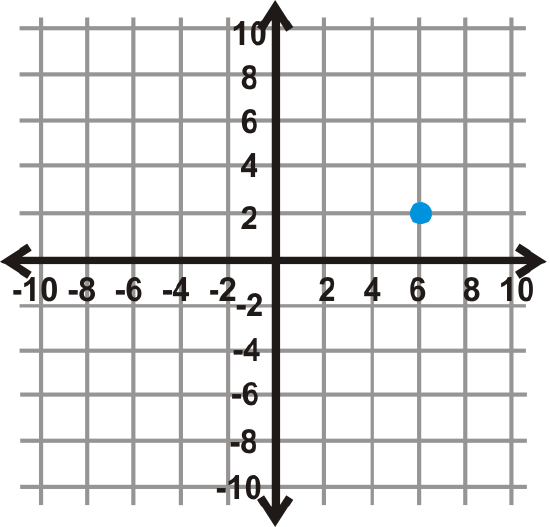
Figure \(\PageIndex{12}\) - \(90^{\circ}\)
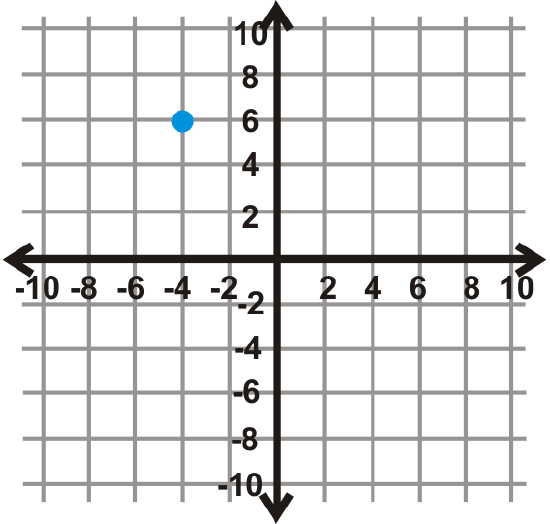Figure \(\PageIndex{13}\) - \(180^{\circ}\)
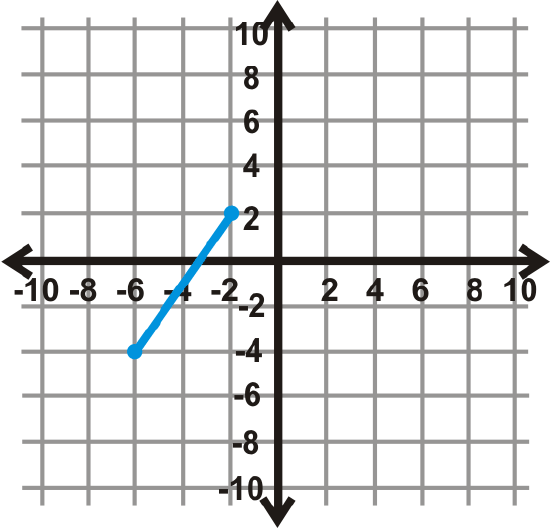
Figure \(\PageIndex{14}\) - \(270^{\circ}\)
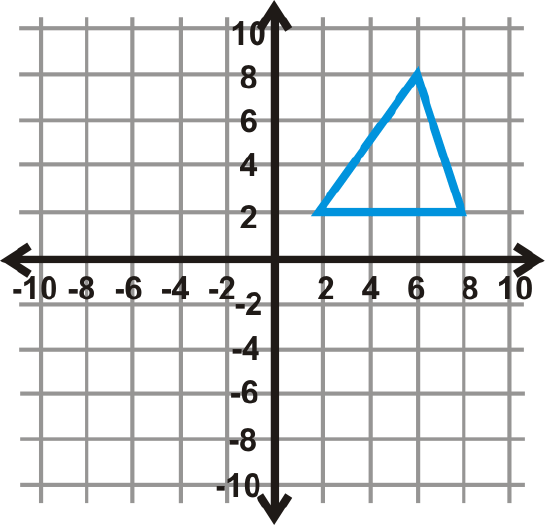
Figure \(\PageIndex{15}\) - \(90^{\circ}\)
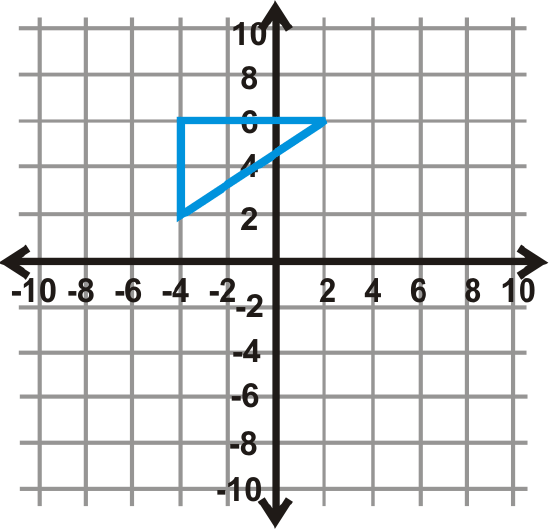
Figure \(\PageIndex{16}\) - \(270^{\circ}\)
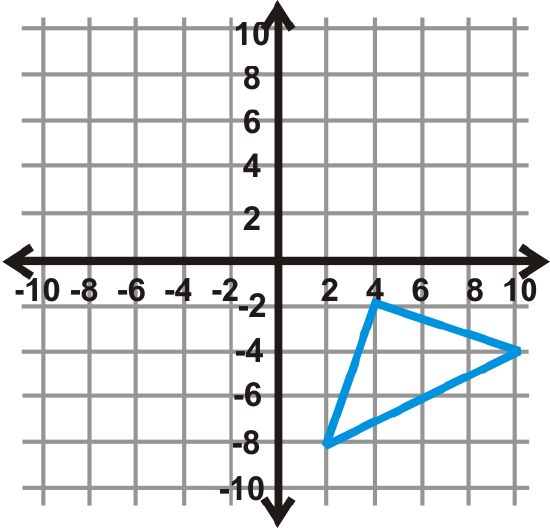
Figure \(\PageIndex{17}\) - \(180^{\circ}\)
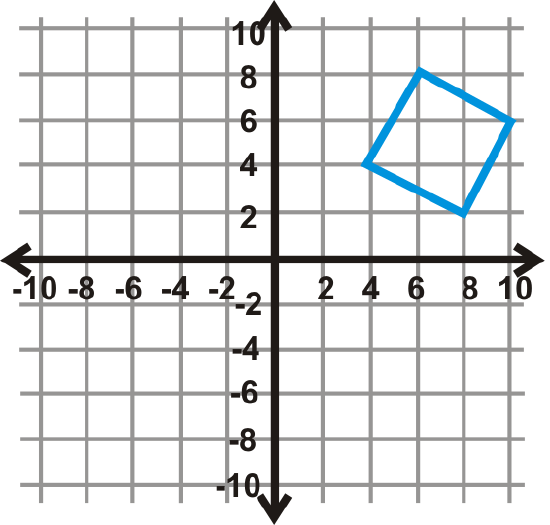
Figure \(\PageIndex{18}\) - \(270^{\circ} \)
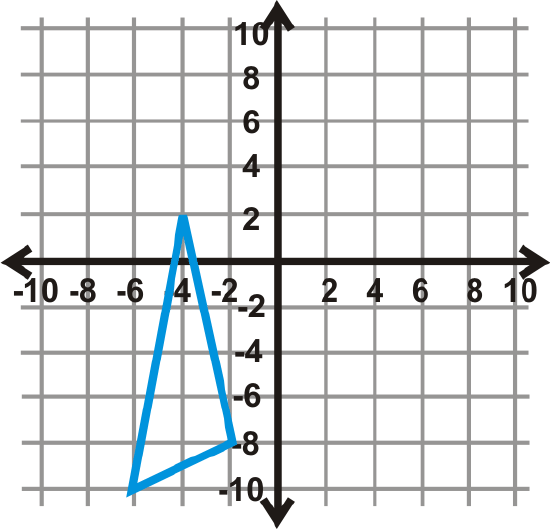
Figure \(\PageIndex{19}\) - \(90^{\circ} \)
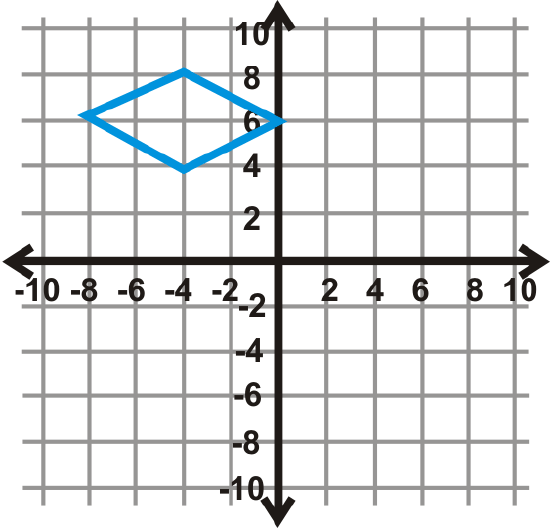
Figure \(\PageIndex{20}\)
Find the measure of \(x\) in the rotations below. The blue figure is the preimage.
-
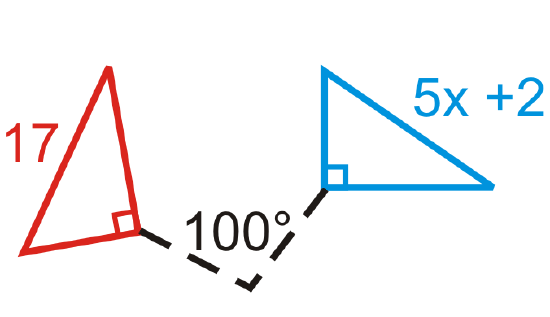
Figure \(\PageIndex{21}\) -
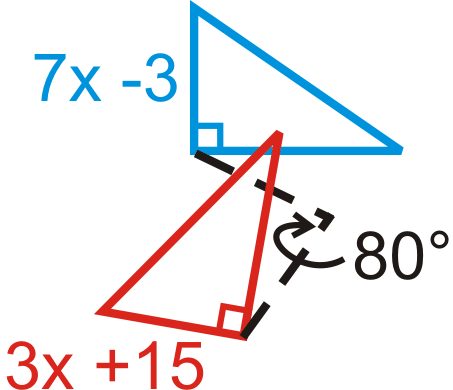
Figure \(\PageIndex{22}\) -
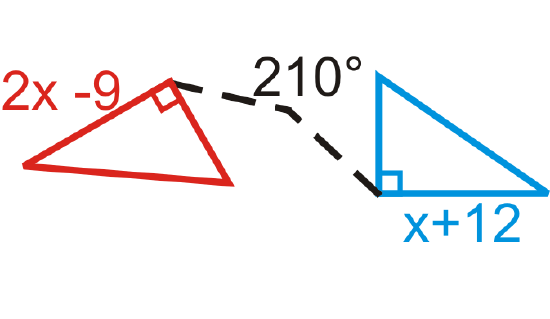
Figure \(\PageIndex{23}\)
Find the angle of rotation for the graphs below. The center of rotation is the origin and the blue figure is the preimage. Your answer will be \(90^{\circ}\), \(270^{\circ}\), or \(180^{\circ}\).
-
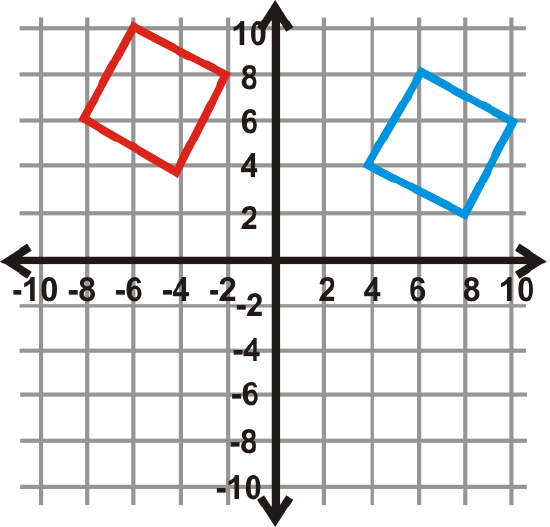
Figure \(\PageIndex{24}\) -
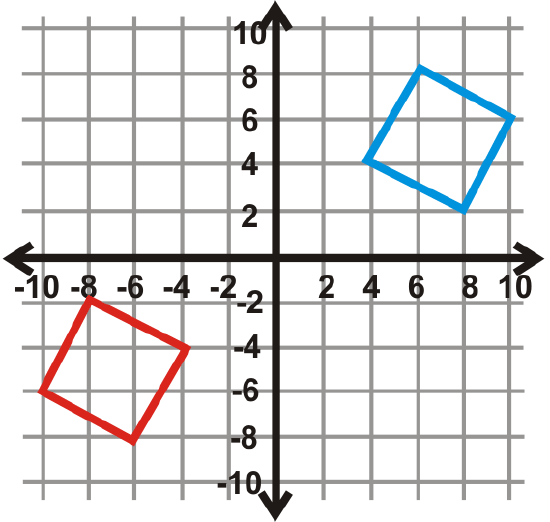
Figure \(\PageIndex{25}\) -
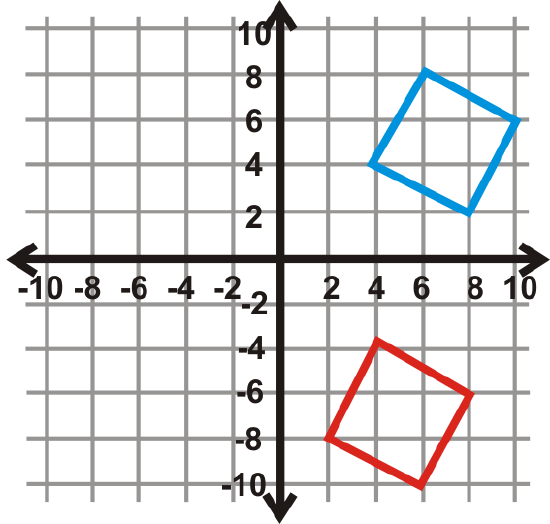
Figure \(\PageIndex{26}\) -
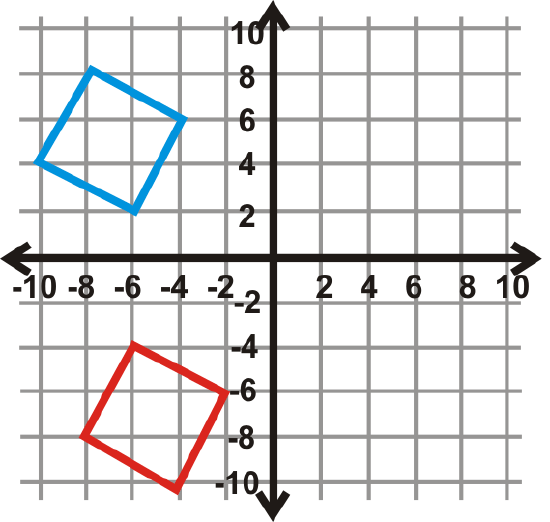
Figure \(\PageIndex{27}\) -
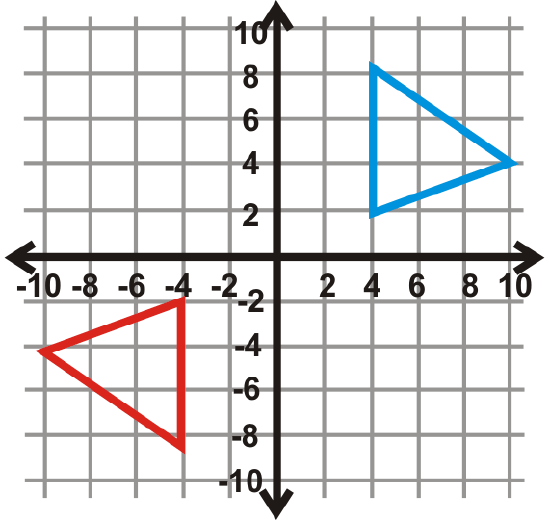
Figure \(\PageIndex{28}\) -
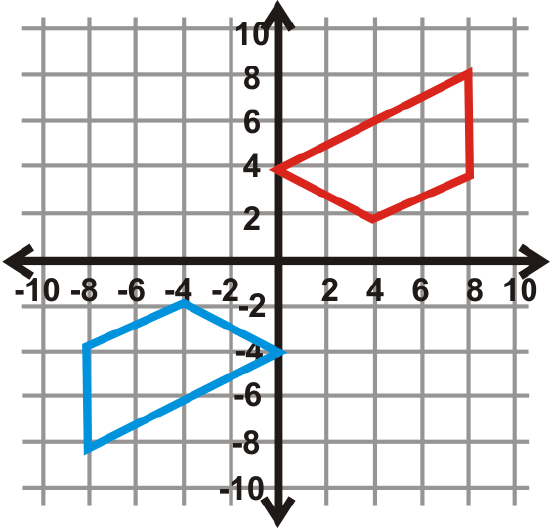
Figure \(\PageIndex{29}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 12.4.
Vocabulary
| Term | Definition |
|---|---|
| Center of Rotation | In a rotation, the center of rotation is the point that does not move. The rest of the plane rotates around this fixed point. |
| Image | The image is the final appearance of a figure after a transformation operation. |
| Origin | The origin is the point of intersection of the x and y axes on the Cartesian plane. The coordinates of the origin are (0, 0). |
| Preimage | The pre-image is the original appearance of a figure in a transformation operation. |
| Rotation | A rotation is a transformation that turns a figure on the coordinate plane a certain number of degrees about a given point without changing the shape or size of the figure. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Transformation: Rotation Principles - Basic
Activities: Rotations Discussion Questions
Study Aids: Types of Transformations Study Guide
Practice: Defining Rotation
Real World: Radical Rotations