8.11: Rotation Rules

State rules that describe given rotations.

Rules for Rotations

The figure below shows a pattern of two fish. Write the mapping rule for the rotation of Image A to Image B.

Figure \(\PageIndex{1}\)

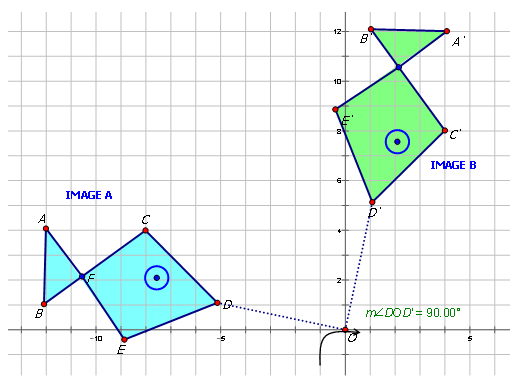
In geometry, a transformation is an operation that moves, flips, or changes a shape to create a new shape. A rotation is an example of a transformation where a figure is rotated about a specific point (called the center of rotation), a certain number of degrees. Common rotations about the origin are shown below:

Center of Rotation	Angle of Rotation	Preimage (Point P)	Rotated Image (Point P′)	Notation (Point P′)
(0, 0)	\(90^{\circ}\)(or \(−270^{\circ}\))	\((x,y)\)	\((−y,x)\)	\((x,y)\rightarrow (−y,x)\)
(0, 0)	\(180^{\circ}\)(or \(−180^{\circ}\))	\((x,y)\)	\((−x,−y)\)	\((x,y)\rightarrow (−x,−y)\)
(0, 0)	\(270^{\circ}\)(or \(−90^{\circ}\))	\((x,y)\)	\((y,−x)\)	\((x,y)\rightarrow (y,−x)\)

You can describe rotations in words, or with notation. Consider the image below:

Figure \(\PageIndex{2}\)

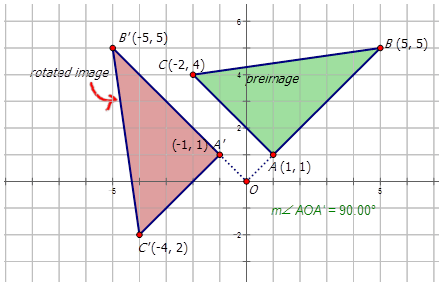
Notice that the preimage is rotated about the origin \(90^{\circ}\)CCW. If you were to describe the rotated image using notation, you would write the following:

\(R_{90^{\circ}}(x,y)=(−y,x)\)

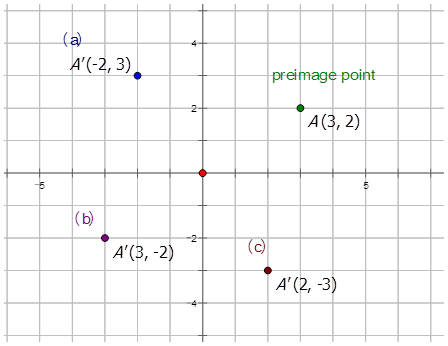
Let's write the notation to describe the following CCW rotations on the point (3, 2)\) and draw the image:

1. about the origin at \(90^{\circ}\)

Rotation about the origin at \(90^{\circ}: \(R_{90^{\circ}}(x,y)=(−y,x)\)

2. about the origin at \(180^{\circ}\)

Rotation about the origin at \(180^{\circ}\): \(R_{180^{\circ}}(x,y)=(−x, −y)\)

3. about the origin at \(270^{\circ}\)

Rotation about the origin at 270^{\circ}: \(R_270^{\circ}(x,y)=(y,−x)\)

Figure \(\PageIndex{3}\)

Now let's perform the following rotations on Image \(A\) shown below in the diagram below and describe the rotations:

Figure \(\PageIndex{4}\)

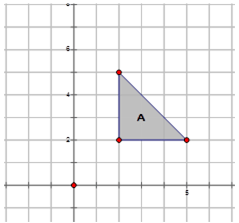
1. about the origin at \(90^{\circ}\), and label it \(B\).

Rotation about the origin at \(90^{\circ}\): \(R_{90^{\circ}}A\rightarrow B=R_{90^{\circ}}(x,y)\rightarrow (−y,x)\)

2. about the origin at \(180^{\circ}\), and label it \(O\).

Rotation about the origin at \(180^{\circ}\): \(R_{180^{\circ}}A\rightarrow O=R_{180^{\circ}}(x,y)\rightarrow (−x,−y)\)

3. about the origin at \(270^{\circ}\), and label it \(Z\).

Rotation about the origin at \(270^{\circ}\): \(R_{270^{\circ}}A\rightarrow Z=R270^{\circ}(x,y)\rightarrow (y,−x)\)

Figure \(\PageIndex{5}\)

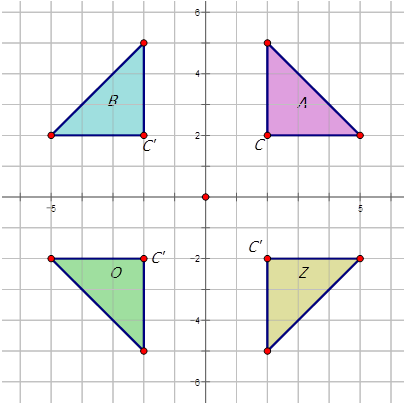
Finally, let's write the notation that represents the rotation of the preimage A to the rotated image J in the diagram below:

Figure \(\PageIndex{6}\)

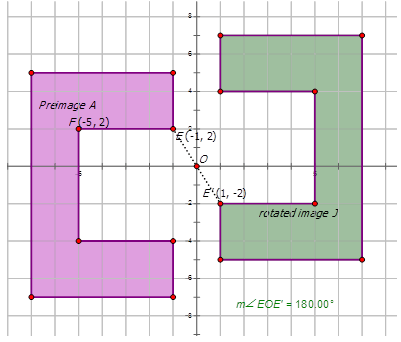
First, pick a point in the diagram to use to see how it is rotated.

\(E:(−1,2)\qquad E′:(1,−2)\)

Notice how both the \(x\)- and \(y\)-coordinates are multiplied by -1. This indicates that the preimage \(A\) is reflected about the origin by \(180^{\circ}\)CCW to form the rotated image J. Therefore the notation is \(R_{180^{\circ}}A\rightarrow J=R_{180^{\circ}}(x,y)\rightarrow (−x,−y)\).

Example \(\PageIndex{1}\)

Earlier, you were given the figure below which shows a pattern of two fish. Write the mapping rule for the rotation of Image \(A\) to Image \(B\).

Figure \(\PageIndex{7}\)

Solution

Notice that the angle measure is \(90^{\circ}\) and the direction is clockwise. Therefore the Image \(A\) has been rotated \(−90^{\circ}\) to form Image \(B\). To write a rule for this rotation you would write: \(R_{270^{\circ}}(x,y)=(−y,x)\).

Example \(\PageIndex{}\)

Thomas describes a rotation as point \(J\) moving from \(J(−2,6)\) to \(J′(6,2)\). Write the notation to describe this rotation for Thomas.

\(J:(−2,6)\qquad J′:(6,2)\)

Figure \(\PageIndex{8}\)

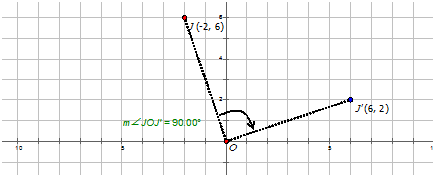
Solution

Since the \(x\)-coordinate is multiplied by -1, the \(y\)-coordinate remains the same, and finally the \(x\)- and \(y\)-coordinates change places, this is a rotation about the origin by \(270^{\circ}\) or \(−90^{\circ}\). The notation is: \(R_{270^{\circ}}J\rightarrow J′=R_270^{\circ}(x,y)\rightarrow (y,−x)\)

Example \(\PageIndex{1}\)

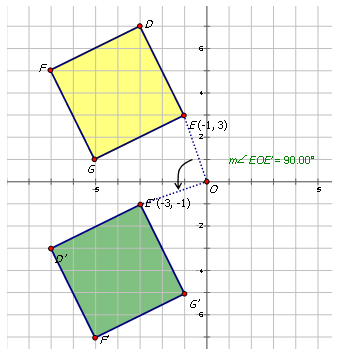
Write the notation that represents the rotation of the yellow diamond to the rotated green diamond in the diagram below.

Figure \(\PageIndex{9}\)

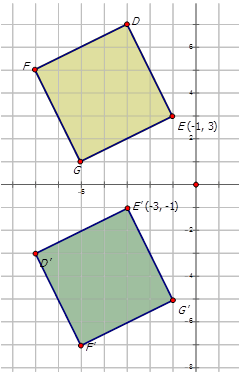
Solution

In order to write the notation to describe the rotation, choose one point on the preimage (the yellow diamond) and then the rotated point on the green diamond to see how the point has moved. Notice that point E\) is shown in the diagram:

\(E(−1,3)\rightarrow E′(−3,−1)\)

Since both \(x\)- and \(y\)-coordinates are reversed places and the \(y\)-coordinate has been multiplied by -1, the rotation is about the origin \(90^{\circ}\). The notation for this rotation would be: \(R_{90^{\circ}}(x,y)\rightarrow (−y,x)\).

Figure \(\PageIndex{10}\)

Example \(\PageIndex{1}\)

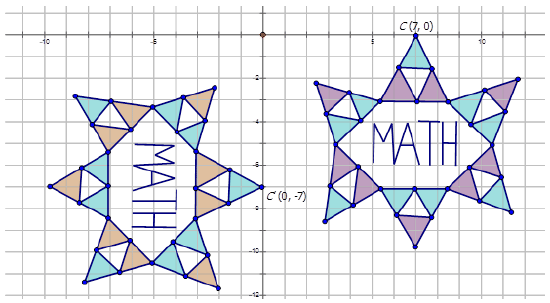
Karen was playing around with a drawing program on her computer. She created the following diagrams and then wanted to determine the transformations. Write the notation rule that represents the transformation of the purple and blue diagram to the orange and blue diagram.

Figure \(\PageIndex{11}\)

Solution

In order to write the notation to describe the transformation, choose one point on the preimage (purple and blue diagram) and then the transformed point on the orange and blue diagram to see how the point has moved. Notice that point \(C\) is shown in the diagram:

\(C(7,0)\rightarrow C′(0,−7)\)

Since the \(x\)-coordinates only are multiplied by -1, and then \(x\)- and \(y\)-coordinates change places, the transformation is a rotation is about the origin by \(270^{\circ}\). The notation for this rotation would be: \(R_{270^{\circ}}(x,y)\rightarrow (y,−x)\).

Review

Complete the following table:

Starting Point	\(90^{\circ}\) Rotation	\(180^{\circ}\) Rotation	\(270^{\circ}\) Rotation	\(360^{\circ}\) Rotation
1. \((1, 4)\)
2. \((4, 2)\)
3. \((2, 0)\)
4. \((-1, 2)\)
5. \((-2, -3)\)

Write the notation that represents the rotation of the preimage to the image for each diagram below.

6. 

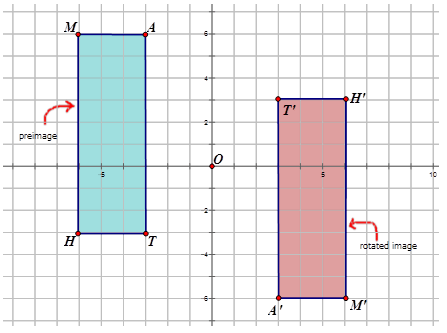
   Figure \(\PageIndex{12}\)

7. 

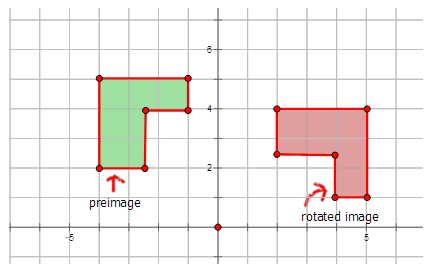
   Figure \(\PageIndex{13}\)

8. 

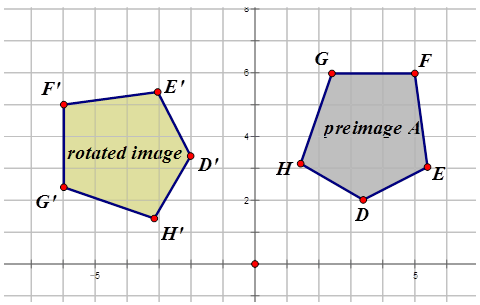
   Figure \(\PageIndex{14}\)

9. 

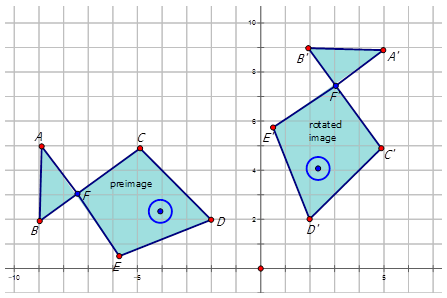
   Figure \(\PageIndex{15}\)

10. 

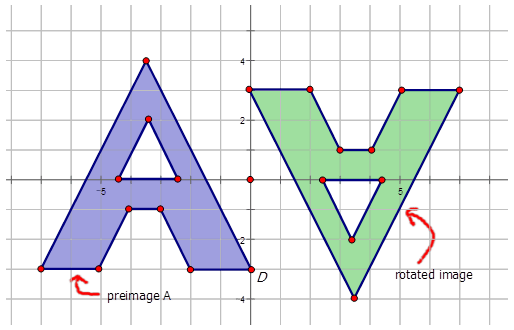
    Figure \(\PageIndex{16}\)

Write the notation that represents the rotation of the preimage to the image for each diagram below.

11. 

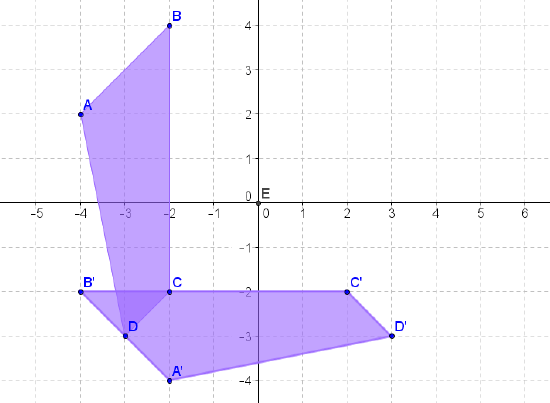
    Figure \(\PageIndex{17}\)

12. 

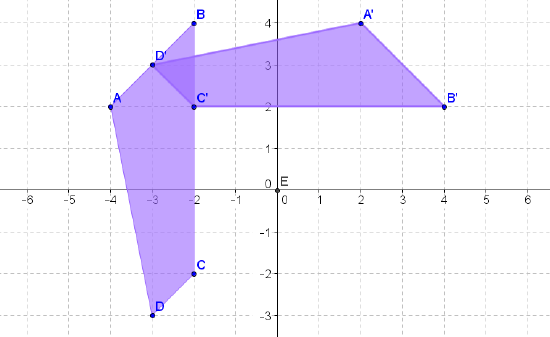
    Figure \(\PageIndex{18}\)

13. 

    Figure \(\PageIndex{19}\)

14. 

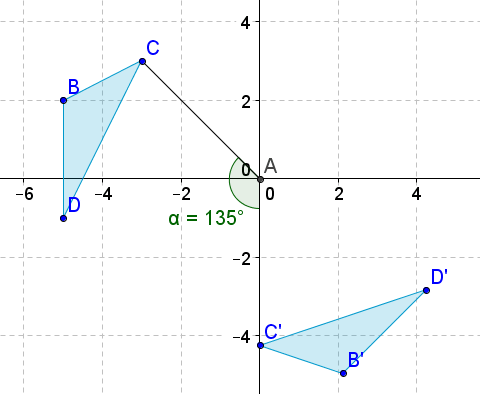
    Figure \(\PageIndex{20}\)

15. 

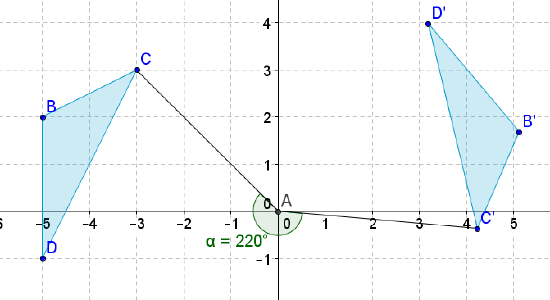
    Figure \(\PageIndex{21}\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 10.9.

Additional Resources

Video: Rules for Rotations

Practice: Rotation Rules