4.19: Midsegment Theorem
- Page ID
- 4816
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Midsegment of a triangle joins the midpoints of two sides and is half the length of the side it is parallel to.
A line segment that connects two midpoints of the sides of a triangle is called a midsegment. \(\overline{DF}\) is the midsegment between \(\overline{AB}\) and \(\overline{BC}\).
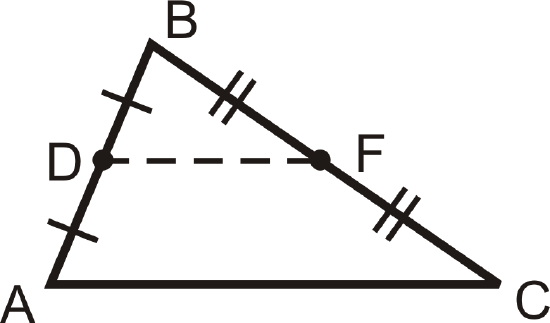
The tic marks show that \(D\) and \(F\) are midpoints. \(\overline{AD}\cong \overline{DB}\) and \(\overline{BF}\cong \overline{FC}\). For every triangle there are three midsegments.
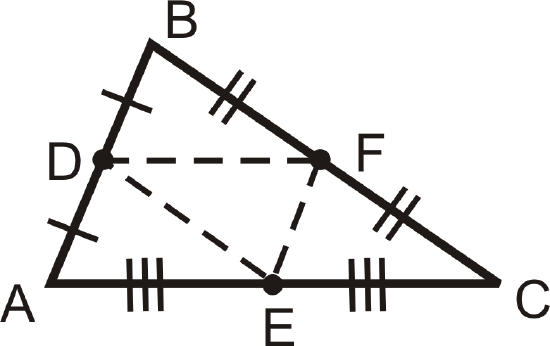
There are two important properties of midsegments that combine to make the Midsegment Theorem. The Midsegment Theorem states that the midsegment connecting the midpoints of two sides of a triangle is parallel to the third side of the triangle, and the length of this midsegment is half the length of the third side. So, if \(\overline{DF}\) is a midsegment of \(\Delta ABC\), then \(DF=\dfrac{1}{2}AC=AE=EC\) and \(\overline{DF} \parallel \overline{AC}\).
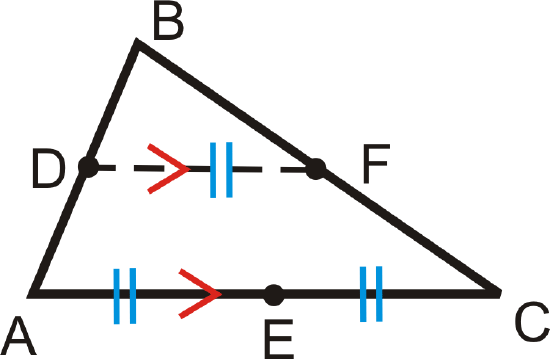
Note that there are two important ideas here. One is that the midsegment is parallel to a side of the triangle. The other is that the midsegment is always half the length of this side.
What if you were given \(\Delta FGH\) and told that \(\overline{JK}\) was its midsegment? How could you find the length of \(JK\) given the length of the triangle's third side, \(FH\)?
Example \(\PageIndex{1}\)
Find the value of \(x\) and AB. \(A\) and \(B\) are midpoints.
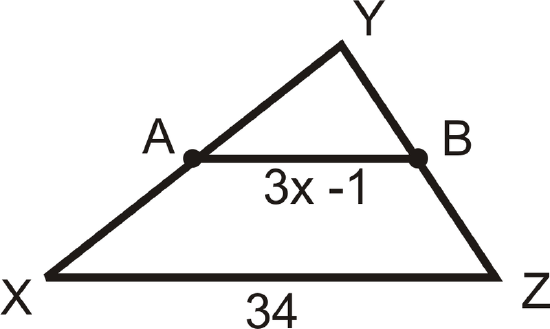
Solution
\(AB=34\div 2=17\). To find \(x\), set \(3x−1\) equal to 17.
\(\begin{align*} 3x−1&=17 \\ 3x&=18 \\ x&=6\end{align*}\)
Example \(\PageIndex{2}\)
True or false: If a line passes through two sides of a triangle and is parallel to the third side, then it is a midsegment.
Solution
This statement is false. A line that passes through two sides of a triangle is only a midsegment if it passes through the midpoints of the two sides of the triangle.
Example \(\PageIndex{3}\)
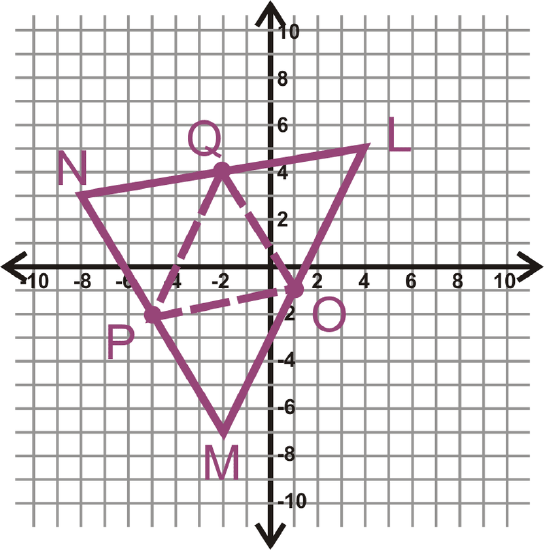
The vertices of \(\Delta LMN\) are \(L(4,5),\: M(−2,−7)\:and\: N(−8,3)\). Find the midpoints of all three sides, label them O, P and Q. Then, graph the triangle, plot the midpoints and draw the midsegments.
Solution
To solve this problem, use the midpoint formula 3 times to find all the midpoints. Recall that the midpoint formula is \(\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)\).
\(L\) and \(M=\left(\dfrac{4+(−2)}{2}, \dfrac{5+(−7)}{2}\right)=(1,−1),\: point\: O\)
\(M\) and \(N=\left(\dfrac{−2+(−8)}{2},\dfrac{−7+3}{2}\right)=(−5,−2),\: point\: P\)
\(L\) and \(N=\left(\dfrac{4+(−8)}{2}, \dfrac{5+3}{2}\right)=(−2,4),\: point\: Q\)
Example \(\PageIndex{4}\)

Mark all the congruent segments on \(\Delta ABC\) with midpoints \(D\), \(E\), and \(F\).
Solution
Drawing in all three midsegments, we have:
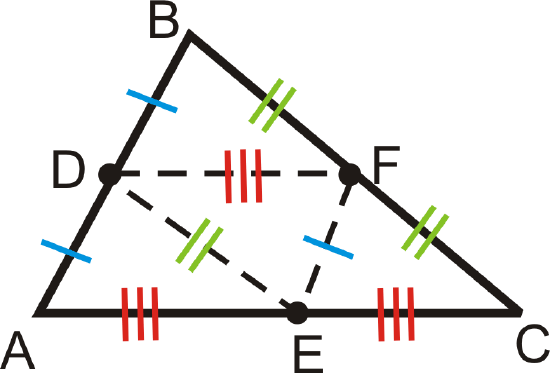
Also, this means the four smaller triangles are congruent by SSS.
Now, mark all the parallel lines on \(\Delta ABC\), with midpoints \(D\), \(E\), and \(F\).
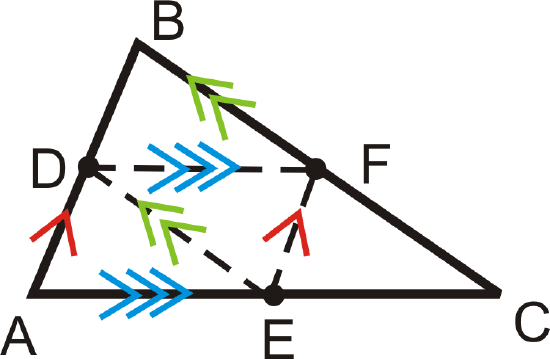
Example \(\PageIndex{5}\)
\(M\), \(N\), and \(O\) are the midpoints of the sides of \(\Delta \(x\)YZ\).
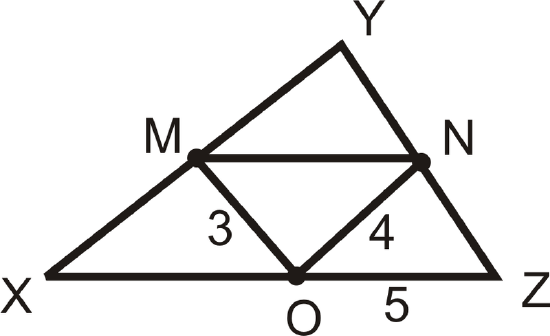
Solution
Find \(MN\), \(XY\), and the perimeter of \(\Delta \(x\)YZ\).
Use the Midsegment Theorem:
\(MN=OZ=5\)
\(XY=2(ON)=2\cdot 4=8\)
Add up the three sides of \(\Delta XYZ\) to find the perimeter.
\(XY+YZ+XZ=2\cdot 4+2\cdot 3+2\cdot 5=8+6+10=24\)
Remember: No line segment over MN means length or distance.
Review
Determine whether each statement is true or false.
- The endpoints of a midsegment are midpoints.
- A midsegment is parallel to the side of the triangle that it does not intersect.
- There are three congruent triangles formed by the midsegments and sides of a triangle.
- There are three midsegments in every triangle.
R, S, T, and U are midpoints of the sides of \(\Delta XPO\) and \(\Delta YPO\)
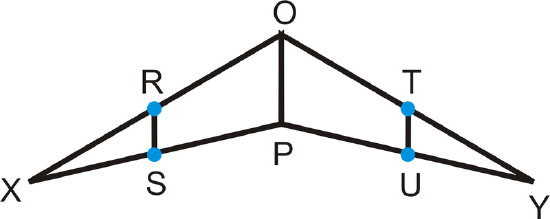
- If \(OP=12\), find \(RS\) and \(TU\).
- If \(RS=8\), find \(TU\).
- If \(RS=2x\), and \(OP=20\), find \(x\) and \(TU\).
- If \(OP=4x\) and \(RS=6x−8\), find \(x\).
For questions 9-15, find the indicated variable(s). You may assume that all line segments within a triangle are midsegments.
-
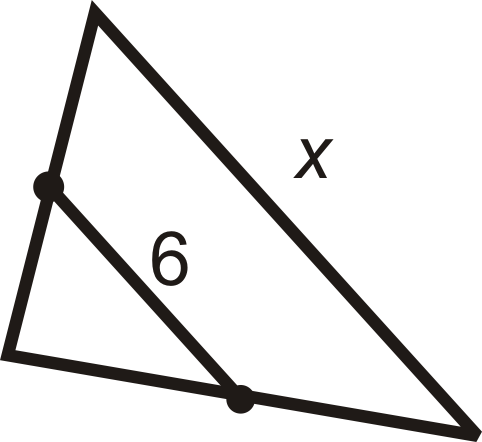
Figure \(\PageIndex{11}\) -
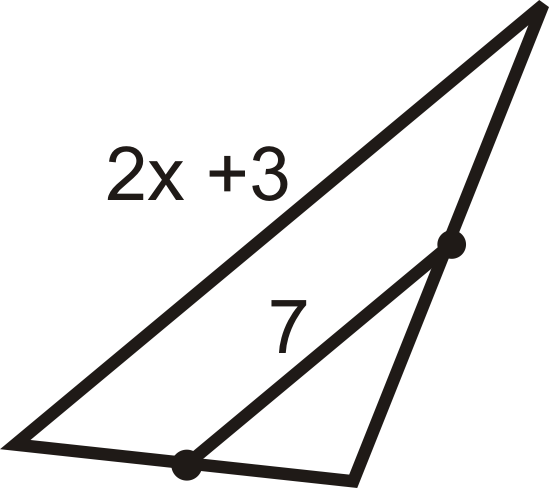
Figure \(\PageIndex{12}\) -
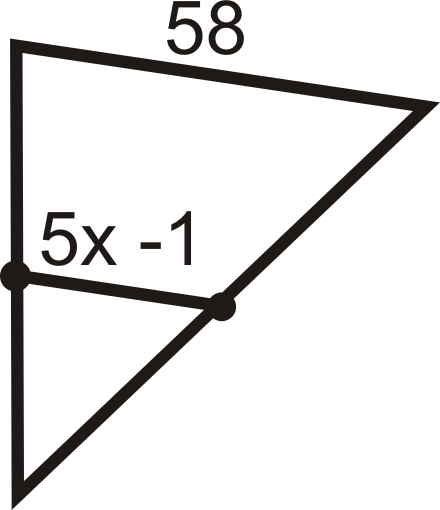
Figure \(\PageIndex{13}\) -
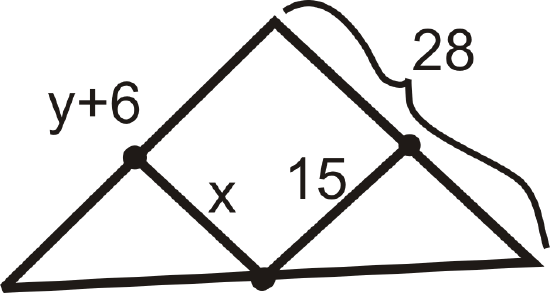
Figure \(\PageIndex{14}\) -
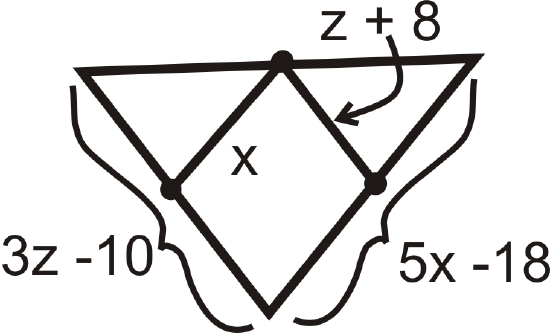
Figure \(\PageIndex{15}\) -
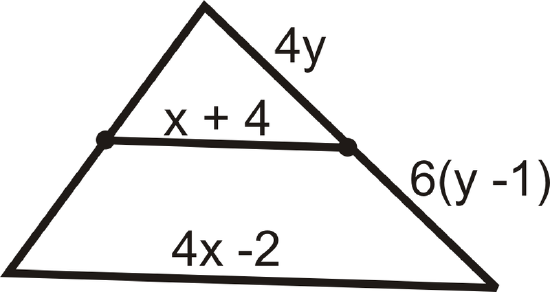
Figure \(\PageIndex{16}\) -
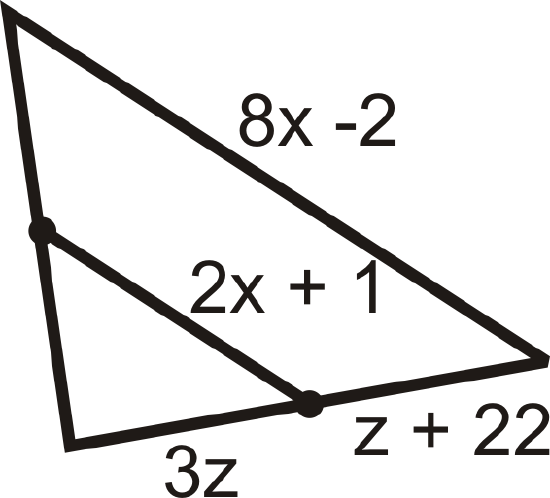
Figure \(\PageIndex{17}\) - The sides of \(\Delta XYZ\) are 26, 38, and 42. \(\Delta ABC\) is formed by joining the midpoints of \(\Delta XYZ\).
- What are the lengths of the sides of \(\Delta ABC\)?
- Find the perimeter of \(\Delta ABC\).
- Find the perimeter of \(\Delta XYZ\).
- What is the relationship between the perimeter of a triangle and the perimeter of the triangle formed by connecting its midpoints?
Coordinate Geometry Given the vertices of \(\Delta ABC\) below find the midpoints of each side.
- \(A(5,−2),\: B(9,4)\: and\: C(−3,8)\)
- \(A(−10,1),\: B(4,11)\: and \:C(0,−7)\)
- \(A(−1,3),\: B(5,7)\: and\: C(9,−5)\)
- \(A(−4,−15),\: B(2,−1)\: and\: C(−20,11)\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.1.
Resources
Vocabulary
| Term | Definition |
|---|---|
| midsegment | A midsegment connects the midpoints of two sides of a triangle or the non-parallel sides of a trapezoid. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Midpoint Formula | The midpoint formula says that for endpoints \((x_1,y_1)\) and \((x_2,y_2)\), the midpoint is (\dfrac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\). |
Additional Resources
Video: Determining Unknown Values Using Properties of the Midsegments of a Triangle
Activities: Midsegment Theorem Discussion Questions
Study Aids: Bisectors, Medians, Altitudes Study Guide
Practice: Midsegment Theorem
Real World: Midsegment Theorem

