4.38: Distance Between Parallel Lines
- Page ID
- 4973
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Length of a perpendicular segment between parallel lines.
All vertical lines are in the form \(x=a\), where \(a\) is the \(x\)-intercept. To find the distance between two vertical lines, count the squares between the two lines. You can use this method for horizontal lines as well. All horizontal lines are in the form \(y=b\), where \(b\) is the \(y\)-intercept.
In general, the shortest distance between two parallel lines is the length of a perpendicular segment between them. There are infinitely many perpendicular segments between two parallel lines, but they will all be the same length.
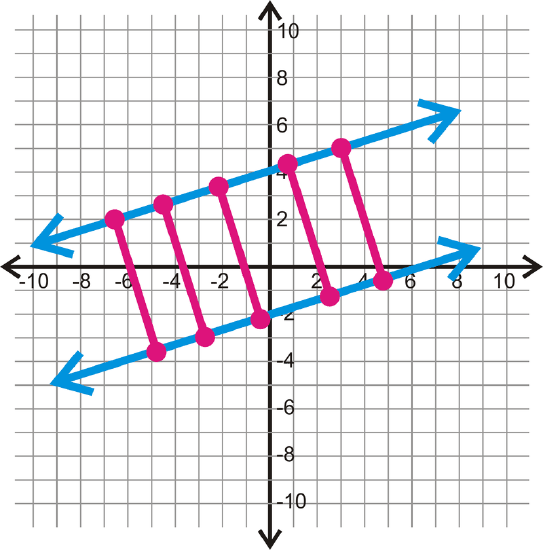
Remember that distances are always positive!
Example \(\PageIndex{1}\)
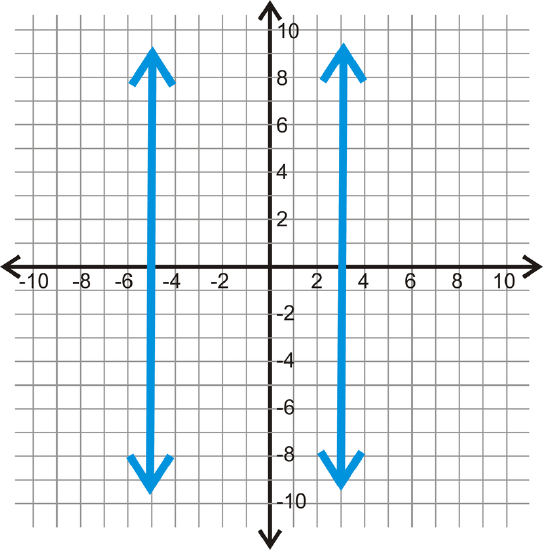
Find the distance between \(x=3\) and \(x=-5\).
Solution
The two lines are \(3 – (-5)\) units apart, or 8 units apart.
Example \(\PageIndex{2}\)
Find the distance between \(x=-5\) and \(x=-10\).
Solution
The two lines are \(-5 – (-10)\) units apart, or 5 units apart.
Example \(\PageIndex{3}\)
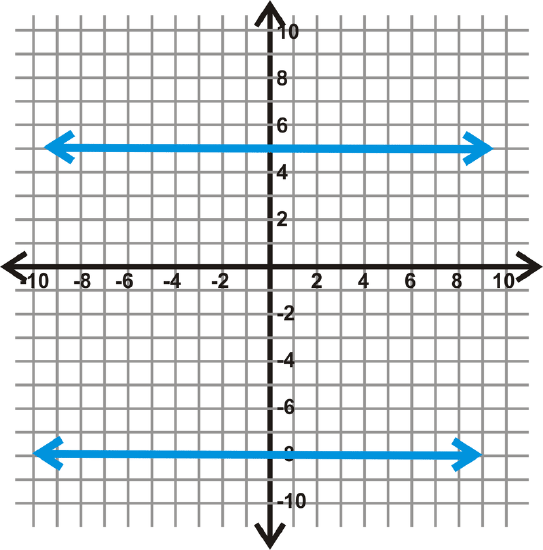
Find the distance between \(y=5\) and \(y=-8\).
Solution
The two lines are \(5 – (-8)\) units apart, or 13 units apart.
Example \(\PageIndex{4}\)
Find the distance between \(y=x+6\) and \(y=x−2\).
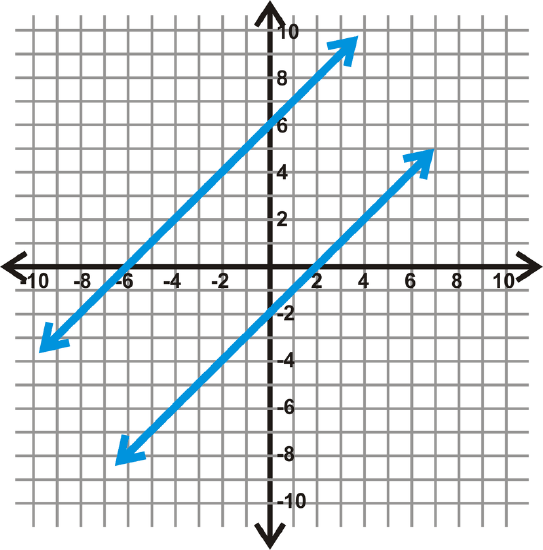
Solution
Step 1: Find the perpendicular slope.
\(m=1\), so \(m_{\perp} =-1\).
Step 2: Find the y-intercept of the top line, \(y=x+6\).
The intercept is \((0, 6)\).
Step 3: Use the slope and count down 1 and to the right 1 until you hit \(y=x−2\).
Always rise/run the same amount for \(m=1\) or \(m=-1\).
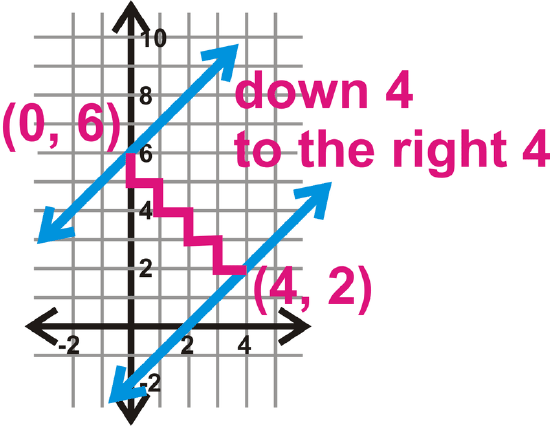
Step 4: Use these two points in the distance formula to determine how far apart the lines are.
\(\begin{align*} d&=\sqrt{(0−4)^2+(6−2)^2} \\ &=\sqrt{(−4)^2+(4)^2} \\ &=\sqrt{16+16} \\ &=\sqrt{32}=5.66\: units\end{align*}\)
Example \(\PageIndex{5}\)
Find the distance between \(y=-x−1\), and \(y=-x−3\).
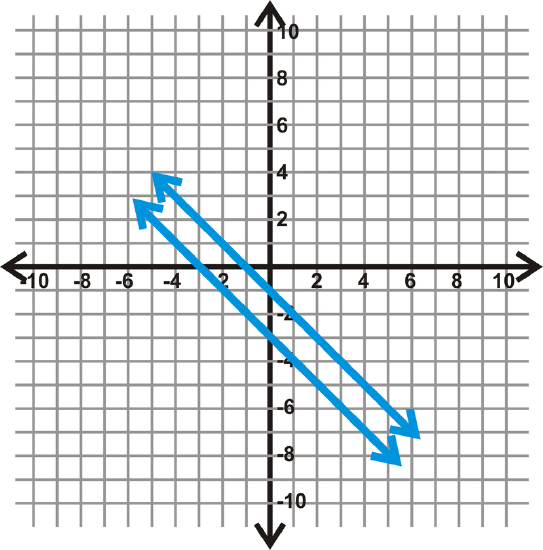
Solution
Step 1: Find the perpendicular slope.
\(m=-1\), so \(m_{\perp} =1\).
Step 2: Find the y-intercept of the top line, \(y=-x−1\).
The intercept is \((0, -1)\).
Step 3: Use the slope and count down 1 and to the left 1 until you hit \(y=x−3\).
Step 4: Use these two points in the distance formula to determine how far apart the lines are.
\(\begin{align*} d&=\sqrt{(0−(-1))^2+(-1−(-2))^2} \\ &=\sqrt{(1)^2+(1)^2} \\ &=\sqrt{1+1} \\ &=\sqrt{2}=1.41\: units \end{align*}\)
Review
Use each graph below to determine how far apart each pair of parallel lines is.
-
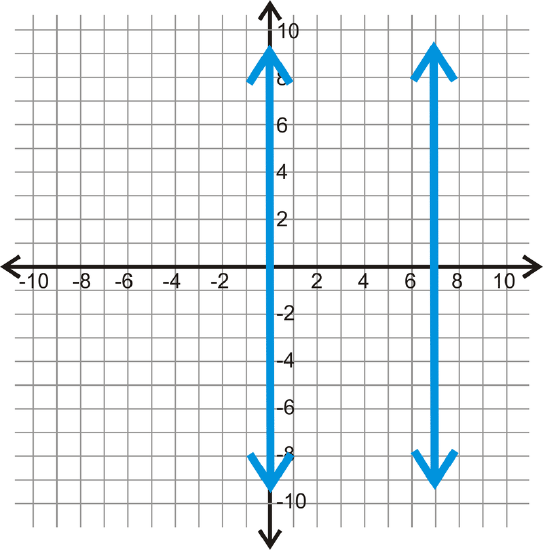
Figure \(\PageIndex{8}\) -
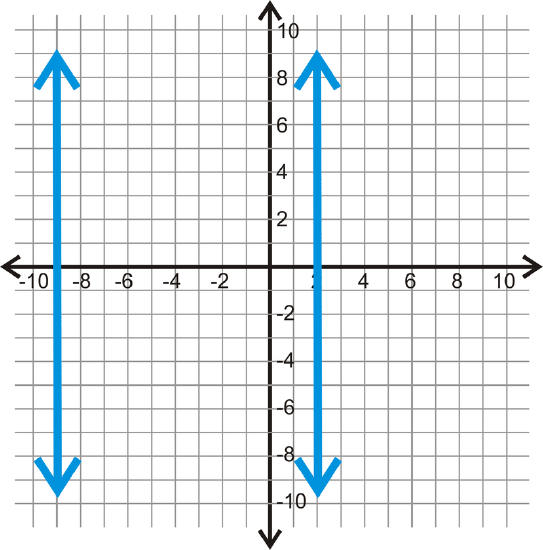
Figure \(\PageIndex{9}\) -
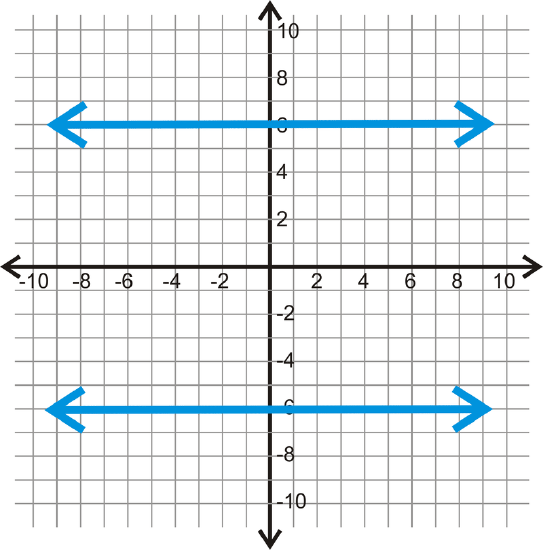
Figure \(\PageIndex{10}\) -
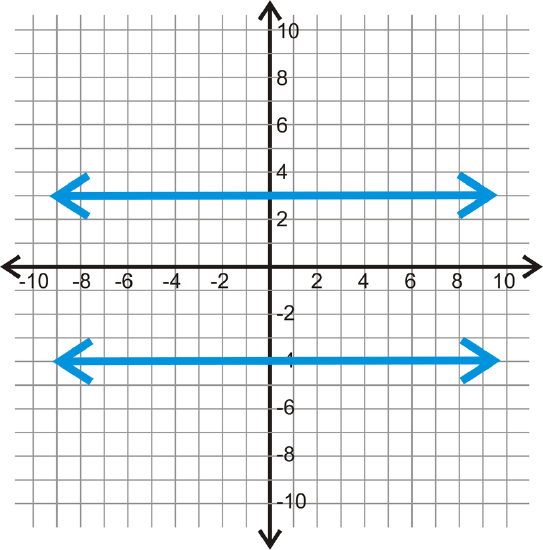
Figure \(\PageIndex{11}\)
Determine the shortest distance between the each pair of parallel lines. Round your answer to the nearest hundredth.
- \(x=5\),\(x=1\)
- \(y=−6\),\(y=4\)
- \(y=3\),\(y=15\)
- \(x=−10\),\(x=−1\)
- \(x=8\),\(x=0\)
- \(y=7\),\(y=−12\)
Find the distance between the given parallel lines.
- \(y=x−3\),\(y=x+11\)
- \(y=−x+4\), \(y=−x\)
- \(y=−x−5\), \(y=−x+1\)
- \(y=x+12\), \(y=x−6\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 3.11.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Distance Formula | The distance between two points \((x_1,y_1)\) and \((x_2,y_2)\) can be defined as \(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). |
| Perpendicular | Perpendicular lines are lines that intersect at a \(90^{\circ}\) angle. The product of the slopes of two perpendicular lines is -1. |
Additional Resources
Interactive Element
Video: Finding The Distance Between Parallel Lines Principles - Basic
Activities: Distance Between Parallel Lines Discussion Questions
Study Aids: Lines in the Coordinate Plane
Practice: Distance Between Parallel Lines
Real World: Flipping Out