4.39: The Distance Formula and Algebra
- Page ID
- 4974
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Using the Pythagorean Theorem to determine distances
Suppose you and your friend were on a scavenger hunt. Starting out from the same place, you walked 5 blocks east and 3 blocks north. Your friend walked 7 blocks west and 2 blocks south. If each block were a tenth of a mile long, could you calculate how far apart you and your friend were? How would you do it?
The Distance Formula
To understand the distance formula, we will first look at the following problem:
Find the length of the segment connecting \((1, 5)\) and \((5, 2)\).
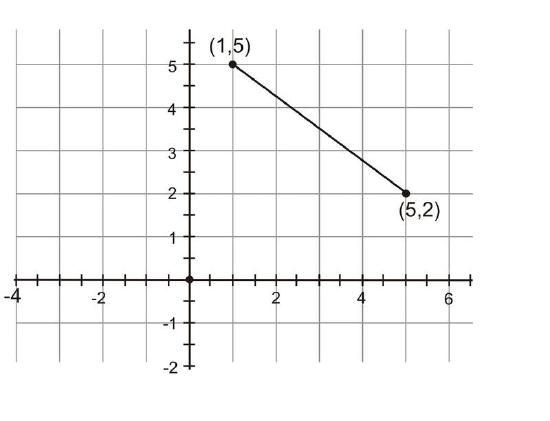
The question asks you to identify the length of the segment. Because the segment is not parallel to either axis, it is difficult to measure given the coordinate grid.
However, it is possible to think of this segment as the hypotenuse of a right triangle. Draw a vertical line and a horizontal line. Find the point of intersection. This point represents the third vertex in the right triangle.
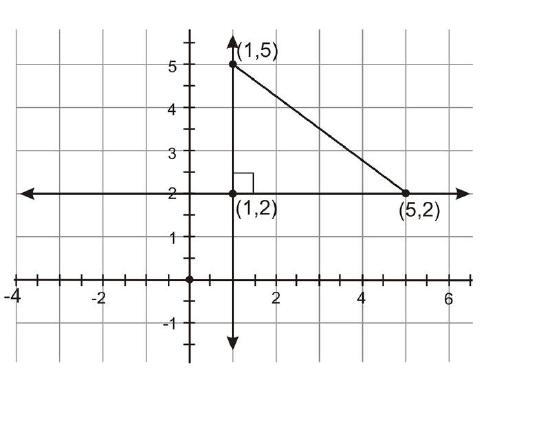
You can easily count the lengths of the legs of this triangle on the grid. The vertical leg extends from \((1, 2)\) to \((1, 5)\), so it is \(\mid5−2\mid=\mid3\mid=3\: units\) long. The horizontal leg extends from \((1, 2)\) to \((5, 2)\), so it is \(\mid5−1\mid=\mid4\mid=4\: units\) long. Use the Pythagorean Theorem with these values for the lengths of each leg to find the length of the hypotenuse.
\(\begin{aligned} a^2+b^2 & =c^2 \\ 3^2+4^2 & =c^2 \\ 9+16 & =c^2 \\ 25 & =c^2 \\ \sqrt{25} & =\sqrt{c^2} \\ 5 & = c\end{aligned}\)
The segment connecting \((1, 5)\) and \((5, 2)\) is 5 units long.
Mathematicians have simplified this process and created a formula that uses these steps to find the distance between any two points in the coordinate plane. If you use the distance formula, you don’t have to draw the extra lines.
The distance formula states: Given points \((x_1,y_1)\) and \((x_2,y_2)\), the length of the segment connecting those two points is \(d=\sqrt{\left(y_{2}-y_{1}\right)^{2}+\left(x_{2}-x_{1}\right)^{2}}\).
Let's use the distance formula to complete the following problems:
- Find the distance between \((–3, 5)\) and \((4, –2)\).
Use the distance formula. Let \((x_1,y_1)=(−3,5)\) and \((x_2,y_2)=(4,−2)\).
\(\begin{array}{l}
d=\sqrt{(-2-5)^{2}+(4-(-3))^{2}} \rightarrow \sqrt{(-7)^{2}+7^{2}} \\
d=\sqrt{98}=7 \sqrt{2} \text { units }
\end{array}\)
- At 8 a.m. one day, Amir decides to walk in a straight line on the beach. After two hours of making no turns and traveling at a steady rate, Amir was two miles east and four miles north of his starting point. How far did Amir walk and what was his walking speed?
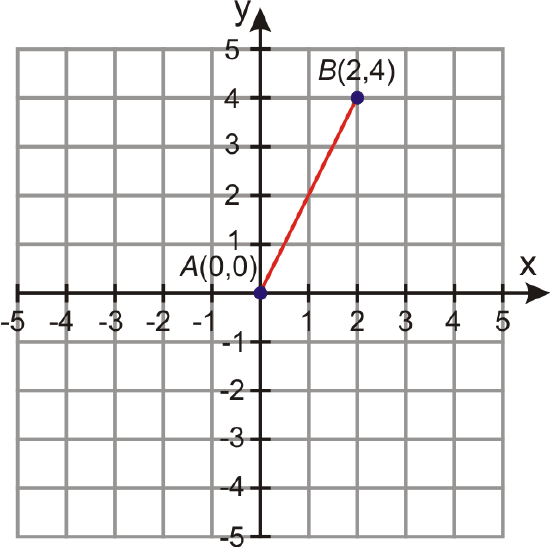
Plot Amir’s route on a coordinate graph. We can place his starting point at the origin, \(A=(0,0)\). Then, his ending point will be at the point \(B=(2,4)\). The distance can be found with the distance formula.
\(\begin{aligned} d&=\sqrt{(4−0)^2+(2−0)^2}=\sqrt{(4)^2+(2)^2}=\sqrt{16+4}=\sqrt{20} \\ d &=4.47\text { miles } \end{aligned} \).
Since Amir walked 4.47 miles in 2 hours, his speed is:
\(Speed=\dfrac{4.47 \text{ miles }}{2 \text{ hours }}=2.24 \: mi/h\)
Example \(\PageIndex{1}\)
Earlier, you were told that on a scavenger hunt, starting out from the same place, you walked 5 blocks east and 3 blocks north and your friend walked 7 blocks west and 2 blocks south. Each block is a tenth of a mile long. How far apart were you and your friend?
Solution
It may be helpful to draw a graph to visualize the situation. Assuming that the starting point was at (0,0) and the distance between each point is equal to one block, if you walked 5 blocks east and 3 blocks north, your coordinates would be \((-5, 3)\). Your friend walked 7 blocks west and 2 blocks south, so their coordinates would be \((7,-2)\)
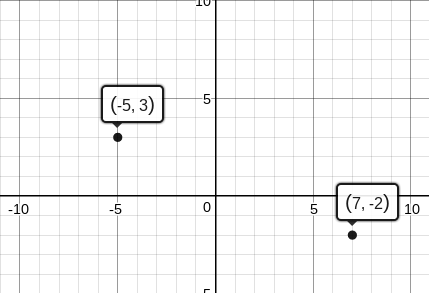
Now, you can calculate the distance between these two points using the distance formula. All you need to do is plug the points into the formula and solve.
\(\begin{aligned} d&=\sqrt{\left(y_{2}-y_{1}\right)^{2}+\left(x_{2}-x_{1}\right)^{2}} \\
d&=\sqrt{(−2−3)^2+(7−(−5))^2}\rightarrow \sqrt{(−5)^2+12^2} \\
d&=\sqrt{169}=13\end{aligned}\)
You and your friend are 13 units away from each other. Since each block is a tenth of a mile long, you can multiply 13 by one tenth to get the actual distance.
\(13 \times \dfrac{1}{10}=\dfrac{13}{10}=1.3\)
You and your friend are 1.3 miles away from each other.
Example \(\PageIndex{2}\)
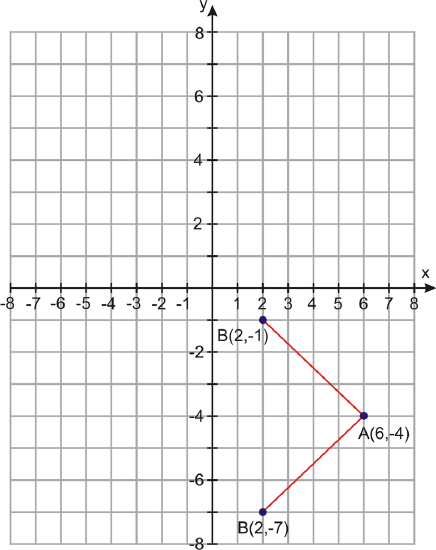
Point \(A=(6,−4)\) and point \(B=(2,k)\). What is the value of \(k\) such that the distance between the two points is 5?
Solution
Use the distance formula.
\(d=\sqrt{(y_1−y_2)^2+(x_1−x_2)^2}\Rightarrow 5=\sqrt{(4−k)^2+(6−2)^2}\)
\(\begin{aligned} Square\: both \:sides \:of \:the \:equation. &\qquad& 5^2&=[\sqrt{(4−k)^2+(6−2)^2}]^2 \\
Simplify.&\qquad& 25&=(−4−k)^2+16 \\ Eliminate\: the \:parentheses. &\qquad& 0&=k^2+8k+16−9 \\
Simplify.&\qquad& 0&=k^2+8k+7 \\
Find \:k \:using \:the \:quadratic \:formula. & \qquad& k&=\dfrac{−8\pm\sqrt{64−28}}{2}=\dfrac{−8\pm\sqrt{36}}{2}=\dfrac{−8\pm6}{2}\end{aligned}\)
\(k=−7\) or \(k=−1\). There are two possibilities for the value of k. Let’s graph the points to get a visual representation of our results.
Review
In 1–10, find the distance between the two points.
- \((x_1,y_1)\) and \((x_2,y_2)\)
- \((7, 7)\) and \((–7, 7)\)
- \((–3, 6)\) and \((3, –6)\)
- \((–3, –1)\) and \((–5, –8)\)
- \((3, –4)\) and \((6, 0)\)
- \((–1, 0)\) and \((4, 2)\)
- \((–3, 2)\) and \((6, 2)\)
- \((0.5, –2.5)\) and \((4, –4)\)
- \((12, –10)\) and \((0, –6)\)
- \((2.3, 4.5)\) and \((–3.4, –5.2)\)
- Find all points having an x-coordinate of –4 and whose distance from point \((4, 2)\) is 10.
- Find all points having a y-coordinate of 3 and whose distance from point \((–2, 5)\) is 8.
- Michelle decides to ride her bike one day. First she rides her bike due south for 12 miles, and then the direction of the bike trail changes and she rides in the new direction for a while longer. When she stops, Michelle is 2 miles south and 10 miles west of her starting point. Find the total distance that Michelle covered from her starting point.
Mixed Review
- Solve \((x−4)^2=121\).
- What is the \(GCF\) of \(21ab^4\) and \(15a^7b^2\)?
- Evaluate \(_10C_7\) and explain its meaning.
- Factor \(6x^2+17x+5\).
- Find the area of a rectangle with a length of \((16+2m)\) and a width of \((12+2m)\).
- Factor \(x^2−81\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.7.
Vocabulary
| Term | Definition |
|---|---|
| Distance Formula | The distance between two points \)(x_1,y_1)\) and \)(x_2,y_2)\) can be defined as \)d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). |
| Midpoint Formula | The midpoint formula says that for endpoints \((x_1,y_1)\) and \((x_2,y_2)\), the midpoint is \((\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2})\). |
Additional Resources
Interactive Element
Video: Distance Formula
Activities: Distance Formula Discussion Questions
Practice: The Distance Formula and Algebra
Real World: SF Map - PythThm

